题目内容
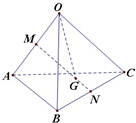已知空间四边形OABC，其对角线为OB，AC，M，N分别是边OA，BC的中点，点G在线段MN上，若MG=λGN，且| OG |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：由题意利用两个向量的加减法及其几何意义可得
=
+
=
•
+
•
+
•
．再根据已知
=
+
+
，可得
=
，由此求得 λ的值．
| OG |
| OM |
| MG |
| 1 |
| 2+2λ |
| OA |
| λ |
| 2+2λ |
| OB |
| λ |
| 2+2λ |
| OC |
| OG |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| 1 |
| 2+2λ |
| 1 |
| 6 |
解答：
解：由题意可得
=
+
=
+
•
=
+
•（
-
）
=
•
+
（
）
=
•
+
•
+
•
．
再根据已知
=
+
+
，则
=
，解得 λ=2，
故选：A．
| OG |
| OM |
| MG |
=
| OM |
| λ |
| 1+λ |
| MN |
=
| OM |
| λ |
| 1+λ |
| ON |
| OM |
=
| 1 |
| 1+λ |
| 1 |
| 2 |
| OA |
| λ |
| 1+λ |
| ||||
| 2 |
=
| 1 |
| 2+2λ |
| OA |
| λ |
| 2+2λ |
| OB |
| λ |
| 2+2λ |
| OC |
再根据已知
| OG |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| 1 |
| 2+2λ |
| 1 |
| 6 |
故选：A．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，属于中档题．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知三个正数a，b，c，满足b＜a+c≤2b，a＜b+c≤2a，则
的取值范围是（ ）
| a |
| b |
A、（
| ||||
B、（
| ||||
C、（0，
| ||||
D、（
|
△ABC外接圆半径等于1，其圆心O满足
=
(
+
)，|
|=|
|，则向量
在
方向上的投影等于（ ）
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| AC |
| BA |
| BC |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知集合A={x∈N|0＜x＜3}，B={x|2x-1＞1}，则A∩B=（ ）
| A、∅ | B、{1} |
| C、{2} | D、{1，2} |
若x，y满足约束条件
，则函数z=2x-y的最大值是（ ）
|
| A、-1 | B、0 | C、3 | D、6 |