题目内容
11.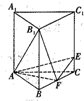 如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.
如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.(Ⅰ)求证:平面B1AF⊥面EAF;
(Ⅱ)求点C1到平面的EAF的距离.
分析 (Ⅰ)由EF⊥B1F,AF⊥EF,可得EF⊥平面B1AF,即可证明平面B1AF⊥面EAF;
(Ⅱ)利用等体积转化,求点C1到平面的EAF的距离.
解答 证明:(Ⅰ)由题意知,在△B1BF和△FCE中,$\frac{B{B}_{1}}{BF}=\frac{FC}{EC}$=2,∠B1BF=∠FCE=$\frac{π}{2}$,
所以△B1BF∽△FCE,
所以∠EFC=∠B1BF,
所以EF⊥B1F.
由直棱柱的性质知:底面ABC⊥侧面BB1C1C,F为BC中点,
所以AF⊥BC,
所以AF⊥侧面侧面BB1C1C,则AF⊥EF.
因为B1F∩AF=F,
所以EF⊥平面B1AF,
所以平面B1AF⊥平面EAF…(6分)
解:(Ⅱ)设点C1到平面AEF的距离为d,
因为S△AEF=$\frac{\sqrt{15}}{4}$,${S}_{EF{C}_{1}}$=$\frac{1}{2}×\frac{3}{2}×1=\frac{3}{4}$
所以由等体积得$\frac{1}{3}×\frac{\sqrt{15}}{4}×d=\frac{1}{3}×\frac{3}{4}×\sqrt{3}$
所以d=$\frac{3\sqrt{5}}{5}$…(12分)
点评 本题考查线面、面面垂直的证明,考查点到平面距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x(x>0)}\\{f(x+1)-f(x+2)(x≤0)}\end{array}\right.$,则f(-2016)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
2.已知A,B,C,D是空间四点,命题p:A,B,C,D四点不共面;命题q:直线AB和CD不相交,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.△ABC的三个内角A,B,C所对边的长分别为a,b,c,设向量$\overrightarrow{p}$=(a+c,b),$\overrightarrow{q}$=(b,c-a).若$\overrightarrow{p}$∥$\overrightarrow{q}$,则角C的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
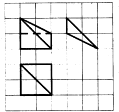 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为$\frac{4}{3}$.
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为$\frac{4}{3}$.