题目内容
16.四棱锥S-ABCD的底面是边长为2的正方形,顶点S在底面的射影是底面正方形的中心O,SO=2,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为$\sqrt{2}+\sqrt{6}$.分析 根据题意可知点P的轨迹为三角形EFG,其中G、F为中点,根据中位线定理求出EF、GE、GF,从而求出轨迹的周长.
解答 解:由题意知,点P的轨迹为如图所示的三角形EFG,其中G、F为中点,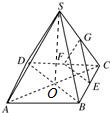
此时AC⊥EF,AC⊥GE,则AC⊥平面EFG,则PE⊥AC.
∵ABCD是边长为2的正方形,∴$BD=2\sqrt{2}$,
∴EF=$\frac{1}{2}$BD=$\sqrt{2}$,
∵SO=2,OB=$\sqrt{2}$,∴$SB=\sqrt{{2}^{2}+(\sqrt{2})^{2}}=\sqrt{6}$,
∴GE=GF=$\frac{1}{2}$SB=$\frac{\sqrt{6}}{2}$,
∴轨迹的周长为$\sqrt{2}+\sqrt{6}$.
故答案为:$\sqrt{2}+\sqrt{6}$.
点评 本题主要考查了轨迹问题,以及点到面的距离等有关知识,同时考查了空间想象能力,计算推理能力,属于中档题.

练习册系列答案
相关题目
14.由变量x与y相对应的一组数据(3,y1),(5,y2),(7,y3),(12,y4),(13,y5)得到的线性回归方程为$\stackrel{∧}{y}$=$\frac{1}{2}$x+20,则$\sum_{i=1}^{5}{y}_{i}$=( )
| A. | 25 | B. | 125 | C. | 120 | D. | 24 |
7.已知双曲线$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{a}$=1的渐近线方程为y=±$\frac{2\sqrt{3}}{3}$x,则此双曲线的离心率是( )
| A. | $\frac{\sqrt{7}}{2}$ | B. | $\frac{\sqrt{13}}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
4.已知A(3,$\sqrt{3}$),O是坐标原点,点P(x,y)的坐标满足$\left\{\begin{array}{l}{\sqrt{3}-y≤0}\\{x-\sqrt{3}+0≥0}\\{y≥0}\end{array}\right.$,设Z为$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影,则Z的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-3,3] | C. | [-$\sqrt{3}$,3] | D. | [-3,$\sqrt{3}$] |
6.下列程序框图中,输出的A的值是( )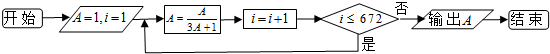
| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{2017}$ | D. | $\frac{1}{2018}$ |
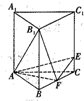 如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.
如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.