题目内容
3.设函数f(x)=tan(2x+$\frac{π}{3}$),则f(x)的定义域为{x|x≠$\frac{π}{12}+\frac{kπ}{2},k∈Z$}.分析 由2x+$\frac{π}{3}$的终边不在y轴上求得x的范围得答案.
解答 解:由2x+$\frac{π}{3}$$≠\frac{π}{2}+kπ$,得x≠$\frac{π}{12}+\frac{kπ}{2},k∈Z$.
∴f(x)的定义域为{x|x≠$\frac{π}{12}+\frac{kπ}{2},k∈Z$}.
故答案为:{x|x≠$\frac{π}{12}+\frac{kπ}{2},k∈Z$}.
点评 本题考查与正切函数有关的复合函数的定义域的求法,是基础题.

练习册系列答案
相关题目
14.定义在R上的偶函数f(x)满足f(x+1)=$\frac{1}{f(x)}$,且f(x)在[-3,-2]上是减函数,若α,β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(sinα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
15.已知$\frac{sinα-2cosα}{3sinα+5cosα}$=5,那么tanα的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{27}{14}$ | D. | -$\frac{23}{16}$ |
12.集合A={1,2,3,4},B={x∈N*|x2-3x-4<0},则A∪B=( )
| A. | {1,2,3} | B. | {1,2,3,4} | C. | {0,1,2,3,4} | D. | (-1,4] |
13.已知坐标原点O(0,0)关于直线L对称的点是M(3,-3),则直线L的方程是( )
| A. | x-2y+1=0 | B. | 2x-y-1=0 | C. | x-y+3=0 | D. | x-y-3=0 |
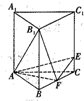 如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.
如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.