题目内容
19.已知函数f(x)=$\frac{1+{3}^{x}}{1-{3}^{x}}$.(Ⅰ)求函数f(x)的定义域和值域;
(Ⅱ)判断函数f(x)的奇偶性,并证明.
分析 (Ⅰ)由1-3x≠0得x≠0,求得函数f(x)的定义域,由3x=$\frac{f(x)-1}{f(x)+1}$>0,求得f(x)的范围,可得f(x)的值域.
(Ⅱ)因为函数f(x)的定义域关于原点对称,且满足f(-x)=-f(x),可得f(x)为奇函数.
解答 解:(Ⅰ)由1-3x≠0得x≠0,
故函数f(x)的定义域为(-∞,0)∪(0,+∞).
由f(x)=$\frac{1+{3}^{x}}{1-{3}^{x}}$,可得3x=$\frac{f(x)-1}{f(x)+1}$>0,
求得f(x)>1,或f(x)<-1,
f(x)的值域为(-∞,-1)∪(1,+∞).
(Ⅱ)f(x)为奇函数,理由如下:
因为函数f(x)的定义域为(-∞,0)∪(0,+∞),
且$f(-x)=\frac{{1+{3^{-x}}}}{{1-{3^{-x}}}}=\frac{{{3^x}+1}}{{{3^x}-1}}=-f(x)$,
所以,f(x)为奇函数.
点评 本题主要考查求函数的定义域和值域,函数的奇偶性的判断方法,属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
17.(x-y)(x+y)8的展开式中x2y7的系数是( )
| A. | -20 | B. | 20 | C. | -22 | D. | 22 |
10.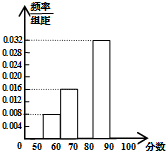 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(Ⅰ)补全频率分布直方图;
(Ⅱ)根据频率分布直方图计算学生成绩的平均值.
 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:(Ⅰ)补全频率分布直方图;
| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | 12 | 0.24 |
| 合计 | 50 | 1 |
7.已知双曲线$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{a}$=1的渐近线方程为y=±$\frac{2\sqrt{3}}{3}$x,则此双曲线的离心率是( )
| A. | $\frac{\sqrt{7}}{2}$ | B. | $\frac{\sqrt{13}}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
14.定义在R上的偶函数f(x)满足f(x+1)=$\frac{1}{f(x)}$,且f(x)在[-3,-2]上是减函数,若α,β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(sinα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
4.已知A(3,$\sqrt{3}$),O是坐标原点,点P(x,y)的坐标满足$\left\{\begin{array}{l}{\sqrt{3}-y≤0}\\{x-\sqrt{3}+0≥0}\\{y≥0}\end{array}\right.$,设Z为$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影,则Z的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-3,3] | C. | [-$\sqrt{3}$,3] | D. | [-3,$\sqrt{3}$] |
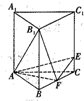 如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.
如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.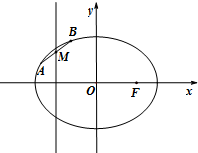 F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线x=-1上.
F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线x=-1上.