题目内容
20.△ABC的三个内角A,B,C所对边的长分别为a,b,c,设向量$\overrightarrow{p}$=(a+c,b),$\overrightarrow{q}$=(b,c-a).若$\overrightarrow{p}$∥$\overrightarrow{q}$,则角C的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
分析 利用向量共线定理、勾股定理的逆定理即可得出.
解答 解:∵$\overrightarrow{p}$∥$\overrightarrow{q}$,
∴b2-(a+c)(c-a)=0,化为:b2+a2=c2,
∴C=$\frac{π}{2}$.
故选:C.
点评 本题考查了向量共线定理、勾股定理的逆定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.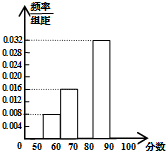 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(Ⅰ)补全频率分布直方图;
(Ⅱ)根据频率分布直方图计算学生成绩的平均值.
 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:(Ⅰ)补全频率分布直方图;
| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | 12 | 0.24 |
| 合计 | 50 | 1 |
15.已知$\frac{sinα-2cosα}{3sinα+5cosα}$=5,那么tanα的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{27}{14}$ | D. | -$\frac{23}{16}$ |
12.集合A={1,2,3,4},B={x∈N*|x2-3x-4<0},则A∪B=( )
| A. | {1,2,3} | B. | {1,2,3,4} | C. | {0,1,2,3,4} | D. | (-1,4] |
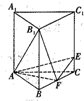 如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.
如图,直棱柱ABC-A1B1C1的棱长都为2,点F为棱BC的中点,点E在棱CC1上,且CC1=4CE.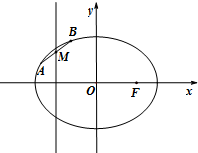 F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线x=-1上.
F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线x=-1上.