题目内容
1.求由A(1,2)、B(0,1)、C(-2,3)三点所确定的圆的方程.分析 设圆的方程为x2+y2+Dx+Ey+F=0,将A、B、C的坐标代入得到关于D、E、F的方程组,解之得到圆的方程.
解答 解:设经过A(1,2),B(0,1),C(-2,3)三点的圆的方程为x2+y2+Dx+Ey+F=0,
∵A(1,2),B(0,1),C(-2,3)三点在圆上,
∴将A、B、C的坐标代入,可得$\left\{\begin{array}{l}{D+2E+F+5=0}\\{E+F+1=0}\\{-2D+3E+F+13=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{D=1}\\{E=-5}\\{F=4}\end{array}\right.$,
故圆的方程为x2+y2+x-5y+4=0.
点评 本题给出经过三点的圆,求圆的方程,着重考查了圆的一般方程、点与圆的位置关系等知识,属于基础题.

练习册系列答案
相关题目
10.函数y=(sinx2)3的导数是( )
| A. | y′=3xsinx2•sin2x2 | B. | y′=3(sinx2)2 | ||
| C. | y′=3(sinx2)2cosx2 | D. | y′=6sinx2cosx2 |
9.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$,则目标函数$z=\frac{y+1}{x+1}$的取值范围是( )
| A. | $[{\frac{1}{2},\frac{5}{2}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{5}{2},+∞})$ |
6.函数y=log4(x+2)的定义域为( )
| A. | {x|x≥-4} | B. | {x|x>-4} | C. | {x|x≥-2} | D. | {x|x>-2} |
10.设i是虚数单位,复数$z=\frac{{{i^5}(2+i)}}{2-i}$,其共轭复数$\overline z$的虚部是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}i$ | C. | -$\frac{3}{5}$ | D. | $-\frac{3}{5}i$ |
11.设直线ax+by+c=0的倾斜角为α,且sinα+cosα=0,则a-b=( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
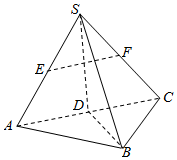 如图,在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.
如图,在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.