题目内容
9．用定积分的几何意义求${∫}_{a}^{b}$$\sqrt{-（x-a）（x-b）}$dx的值（b＞a）．分析 根据定积分几何意义转化为求对应曲线围成的面积即可．
解答 解：y=$\sqrt{-（x-a）（x-b）}$，a≤x≤b，
∴y2=-（x-a）（x-b），
∴（x-$\frac{a+b}{2}$）2+y2=（$\frac{b-a}{2}$）2，
则表示以（$\frac{a+b}{2}$，0）为圆心，以$\frac{b-a}{2}$为半径的圆，
∴${∫}_{a}^{b}$$\sqrt{-（x-a）（x-b）}$dx表示圆的面积的二分之一，
∴${∫}_{a}^{b}$$\sqrt{-（x-a）（x-b）}$dx=$\frac{1}{2}$π（$\frac{b-a}{2}$）2=$\frac{π（b-a）^{2}}{8}$
点评 本题主要考查定积分、定积分的几何意义、圆的标准方程，考查考查数形结合思想．属于基础题．
练习册系列答案
相关题目
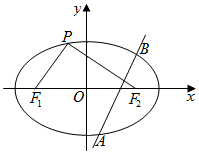已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率e=$\frac{{\sqrt{2}}}{2}$，P为椭圆E上的任意一点（不含长轴端点），且△PF1F2面积的最大值为2．
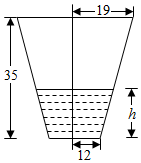降水量是指水平地面上单位面积的降水的深度，用上口直径为38cm，底面直径为24cm，深为35cm的圆台形水桶（轴截面如图）来测量降水量，如果在一次降雨过程中，用此桶盛得的雨水正好是桶深的$\frac{1}{7}$，求这次降雨的降水量（精确到1mm）．