题目内容
16.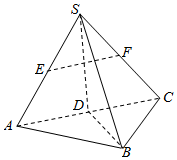 如图,在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.
如图,在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.(1)求证:EF∥平面ABC;
(2)若SA=SC,BD⊥平面SAC,求证:平面SBD⊥平面ABC.
分析 (1)利用中位线定理证明EF∥AC,继而EF∥平面ABC;
(2)由BD⊥平面SAC得BD⊥SD,由等腰三角形三线合一得SD⊥AC,故SD⊥平面ABC,得出平面SBD⊥平面ABC.
解答 证明:(1)∵E、F分别为棱SA、SC的中点,
∴EF∥AC,又∵EF?平面ABC,AC?平面ABC,
∴EF∥平面ABC.
(2)∵SA=SC,D是AC中点,
∴SD⊥AC,
∵BD⊥平面SAC,SD?平面SAC,
∴SD⊥BD,又AC?平面ABC,BD?平面ABC,AC∩BD=D,
∴SD⊥平面ABC,∵SD?平面SBD,
∴平面SBD⊥平面ABC.
点评 本题考查了线面平行的判定,线面垂直的性质,面面垂直的判定,属于中档题.

练习册系列答案
相关题目
4.下列命题中的假命题是( )
| A. | ?x∈R,lg x=1 | B. | ?x∈R,tan x=1 | C. | ?x∈R,x3>0 | D. | ?x∈R,2x>0 |
11.已知直线方程y-3=$\sqrt{3}$(x-4),则这条直线的倾斜角是( )
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
5.设x3+ax+b=0,其中a,b均为实数.下列条件中不能使得该三次方程仅有一个实根的是( )
| A. | a=-3,b=~3 | B. | a=0,b=2 | C. | a=-3,b=2 | D. | a=1 b=2 |