题目内容
已知一组数x1,x2,…,xn的方差是4,则2x1-1,2x2-1,…,2xn-1的标准差是 .
考点:极差、方差与标准差
专题:概率与统计
分析:设出x1,x2,…,xn的平均数
,方差s2;求出2x1-1,2x2-1,…,2xn-1的平均数
与方差s′2,即得标准差.
. |
| x |
. |
| x′ |
解答:
解:设x1,x2,…,xn的平均数是
=
(x1+x2+…+xn),
方差是s2=
[(x1-
)2+(x2-
)2+…+(xn-
)2]=4;
∴2x1-1,2x2-1,…,2xn-1的平均数是
=
[(2x1-1)+(2x2-1)+..+(2xn-1)]=
[2(x1+x2+…+xn)-n]=2
-1,
∴方差是s′2=
[(2x1-1-2
+1)2+(2x2-1-2
+1)2+…+(2xn-1-2
+1)2]
=
[(x1-
)2+(x2-
)2+…+(xn-
)2]=4s2=4×4=16;
∴标准差是s′=4.
故答案为:4.
. |
| x |
| 1 |
| n |
方差是s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
∴2x1-1,2x2-1,…,2xn-1的平均数是
. |
| x′ |
| 1 |
| n |
| 1 |
| n |
| x |
∴方差是s′2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 4 |
| n |
. |
| x |
. |
| x |
. |
| x |
∴标准差是s′=4.
故答案为:4.
点评:本题考查了求数据的平均数与方差的问题,解题时应根据平均数与方差的定义进行解答,是基础题.

练习册系列答案
相关题目
三个人独立地破译一个密码,他们能单独译出的概率分别为
,
,
,假设他们破译密码是彼此独立的,则此密码被破译出的概率为( )
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
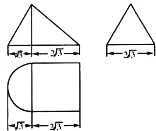 一个几何体的三视图如图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )A、12+
| ||
B、36+
| ||
C、18+
| ||
D、6+
|