Question

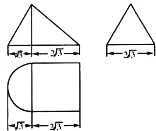一个几何体的三视图如图所示，且其左视图是一个等边三角形，则这个几何体的体积为（　　）

• A、12+

  3π

  2

• B、36+

  9π

  2

• C、18+

  9π

  4

• D、6+

  3π

  4

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由三视图可知，该几何体是一全以俯视图为底面的锥体，求出底面面积和高，代入锥体体积公式，进而可得答案．

解答： 解：由三视图可知，该几何体是一全以俯视图为底面的锥体，
∵几何体的左视图是一个等边三角形，
故锥体的底面是一个边长为2

3

的正方形和一个直径为2

3

的半圆，
故锥体的底面面积S=（2

3

）²+

1

2

π(

2 3

2

)2=12+

3π

2

，
锥体的高h=3，
故锥体的体积V=

1

3

Sh=12+

3π

2

，
故选：A

点评：本题考查的知识点是由三视图，求体积，其中根据已知分析出几何体的形状是解答的关键．