题目内容
已知点A,D分别是椭圆C:
+
=1(a>b>0)的左顶点和上顶点,椭圆的左右焦点分别是F1和F2,点P是线段AD上的动点,如果
•
的最大值2,最小值是-
,那么,椭圆的C的标准方程是 .
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 2 |
| 3 |
考点:椭圆的标准方程
专题:向量与圆锥曲线
分析:画出图形,结合图形,求出线段AD的方程,写出
•
的表达式,根据它表示的几何意义,
得出P在A点时,
•
最大,P在点O到直线AD的距离时,
•
最小,求出a2与b2,即得椭圆的方程.
| PF1 |
| PF2 |
得出P在A点时,
| PF1 |
| PF2 |
| PF1 |
| PF2 |
解答:
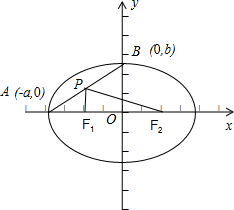 解:∵画出图形,如图所示;
解:∵画出图形,如图所示;
∴直线AD的方程是
+
=1,x∈[-a,0];
∴
=(-c-x,-y),
=(c-x,-y),
•
=x2-c2+y2=x2+y2-c2;
设t=x2+y2,则
表示点P到原点O的距离,
∴当P在A点时,
最大,
此时
•
=(-a)2-02-c2=b2=2;
当P在点O到直线AD的距离时,
最小,
此时
=
,
∴t=
=
,
∴
•
=
-(a2-2)=-
,
整理得3a4-8a2-16=0,
解得a2=4,或a2=-
(舍去);
综上,a2=4,b2=2,
椭圆的方程是
+
=1.
故答案为:
+
=1.
 解:∵画出图形,如图所示;
解:∵画出图形,如图所示;∴直线AD的方程是
| x |
| -a |
| y |
| b |
∴
| PF1 |
| PF2 |
| PF1 |
| PF2 |
设t=x2+y2,则
| t |
∴当P在A点时,
| t |
此时
| PF1 |
| PF2 |
当P在点O到直线AD的距离时,
| t |
此时
| t |
| 1 | ||||||
|
∴t=
| a2b2 |
| a2+b2 |
| 2a2 |
| a2+2 |
∴
| PF1 |
| PF2 |
| 2a2 |
| a2+2 |
| 2 |
| 3 |
整理得3a4-8a2-16=0,
解得a2=4,或a2=-
| 4 |
| 3 |
综上,a2=4,b2=2,
椭圆的方程是
| x2 |
| 4 |
| y2 |
| 2 |
故答案为:
| x2 |
| 4 |
| y2 |
| 2 |
点评:本题考查了向量与椭圆的应用问题,也考查了直线与椭圆的应用问题,考查了求最值的问题,是综合题.

练习册系列答案
相关题目
已知抛物线C:y2=4x,直线l过定点M(a,0),a>0且与抛物线交于A、B两点,O为坐标原点,若∠AOB为锐角,则实数a的取值范围是( )
| A、0<a<4 | B、a>4 |
| C、a≥2 | D、0<a<2 |
设
,
,
为单位向量,
,
的夹角为60°,则(
+
)•
的最大值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
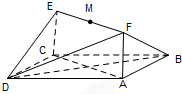 如图所示,已知矩形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知矩形ABCD和矩形ACEF所在的平面互相垂直,AB=