题目内容
设点P在双曲线
-
=1（a＞0，b＞0）的右支上，双曲线两焦点F1、F2，|PF1|=4|PF2|，求双曲线离心率的取值范围．
| x2 |
| a2 |
| y2 |
| b2 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先根据双曲线定义可知|PF1|-|PF2|=2a进而根据|PF1|=4|PF2|，求得2a=3|PF2|，同时利用三角形中两边之和大于第三边的性质，推断出，|F1F2|＜|PF1|+|PF2|，进而求得a和c的不等式关系，分析当p为双曲线顶点时，
=
且双曲线离心率大于1，最后综合答案可得．
| c |
| a |
| 5 |
| 3 |
解答：
解根据双曲线定义可知|PF1|-|PF2|=2a，即4|PF1|-|PF1|=2a．
∴|PF1|=
，|PF2|=
在△PF1F2中，|F1F2|＜|PF1|+|PF2|，
2c＜5|PF2||，c＜
|PF2|=
a，
∴
＜
，
当p为双曲线顶点时，
=
又∵双曲线e＞1，
∴1＜e≤
，
故双曲线离心率的取值范围为：（1，
]
∴|PF1|=
| 8a |
| 3 |
| 2a |
| 3 |
在△PF1F2中，|F1F2|＜|PF1|+|PF2|，
2c＜5|PF2||，c＜
| 5 |
| 2 |
| 5 |
| 3 |
∴
| c |
| a |
| 5 |
| 3 |
当p为双曲线顶点时，
| c |
| a |
| 5 |
| 3 |
又∵双曲线e＞1，
∴1＜e≤
| 5 |
| 3 |
故双曲线离心率的取值范围为：（1，
| 5 |
| 3 |
点评：本题主要考查了双曲线的简单性质，三角形边与边之间的关系．解题的时候一定要注意点P在椭圆顶点位置时的情况，以免遗漏答案．
练习册系列答案
相关题目
已知a=
，函数f（x）=ax，若实数m，n满足f（m）＞f（n），则m、n满足的关系为（ ）
| ||
| 2 |
| A、m+n＜0 | B、m+n＞0 |
| C、m＞n | D、m＜n |
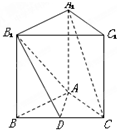如图，底面是正三角形的直三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=2．
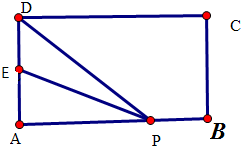如图，在矩形ABCD中，E是AD的中点，P是AB边上的点，AB=3，AD=2