题目内容
9.已知等比数列{an}的前n项和为Sn,若S2=6,S4=30,则S6=( )| A. | 115 | B. | 116 | C. | 125 | D. | 126 |
分析 由等比数列的性质知S2,S4-S2,S6-S4成等比数列,从而解得.
解答 解:∵Sn是等比数列{an}的前n项和,
∴S2,S4-S2,S6-S4成等比数列,
∴(30-6)2=6(S6-S4),
∴S6-S4=24×4=96,
∴S6=96+30=126.
故选:D.
点评 本题考查了等比数列的性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.△ABC中,AC=BC=1,AC⊥BC,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,则下列结论正确的是( )
| A. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=1 | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{5}{2}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=-2 |
20.已知函数f(x)=x3-3ax+$\frac{1}{4}$,若x轴为曲线y=f(x)的切线,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{3}{4}$ | D. | $\frac{1}{4}$ |
17.如图中的程序框图表示求三个实数a,b,c中最大数的算法,那么在空白的判断框中,应该填入( )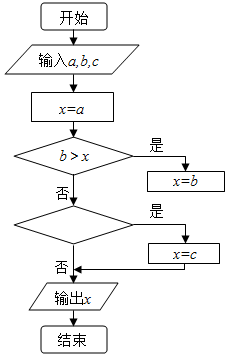

| A. | a>x | B. | b>x | C. | c<x | D. | c>x |
4.在等差数列{an}中,a5+a6=10,则其前10项和S10的值是( )
| A. | 10 | B. | 50 | C. | 60 | D. | 100 |
14.执行如图所示程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
1.已知双曲线C的左右焦点为F1,F2,P双曲线右支上任意一点,若以F1为圆心,以$\frac{1}{2}$|F1F2|为半径的圆与以P为圆心,|PF2|为半径的圆相切,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | $\sqrt{3}$ |
