题目内容
20.△ABC中,AC=BC=1,AC⊥BC,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,则下列结论正确的是( )| A. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=1 | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{5}{2}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=-2 |
分析 由题意可得AB=$\sqrt{2}$,即有|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,且$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\sqrt{2}$×1×$\frac{\sqrt{2}}{2}$=1,求得$\overrightarrow{a}$•$\overrightarrow{b}$=1-2=-1,|$\overrightarrow{b}$|=1,再由向量的平方即为模的平方,计算可得A,B,C不正确,D正确.
解答 解:由AC=BC=1,AC⊥BC,可得AB=$\sqrt{2}$,
即有|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,
且$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\sqrt{2}$×1×$\frac{\sqrt{2}}{2}$=1,
即$\overrightarrow{a}$2+$\overrightarrow{a}$•$\overrightarrow{b}$=1,可得$\overrightarrow{a}$•$\overrightarrow{b}$=1-2=-1,
由|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,可得$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=1,
可得$\overrightarrow{b}$2=1-2+2=1,即|$\overrightarrow{b}$|=1,
则|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$=$\sqrt{2-2×(-1)+1}$=$\sqrt{5}$,
则A不正确;
($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{b}$2=-1-1=-2,则B不正确;
($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\overrightarrow{a}$2-$\overrightarrow{b}$2=2-1=1,则C不正确;
($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{b}$2=-1-1=-2,则D正确.
故选:D.
点评 本题考查向量的数量积的定义和性质,主要是向量的平方即为模的平方,考查化简整理的运算能力,属于中档题.

| A. | 2$\sqrt{3}$-1 | B. | 2$\sqrt{3}$+1 | C. | 4 | D. | $\sqrt{6}$+$\sqrt{2}$+1 |
| A. | 115 | B. | 116 | C. | 125 | D. | 126 |
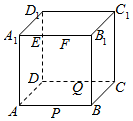 如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法:
如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法: