题目内容
18.已知向量$\overrightarrow a$=(1,x),$\overrightarrow b$=(x-3,2),且$\overrightarrow a$⊥$\overrightarrow b$.(Ⅰ)求x的值;
(Ⅱ)试确定实数k的值,使k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$平行.
分析 (Ⅰ)利用向量的垂直,列出方程,即可求出x值.
(Ⅱ)求出向量,利用向量共线列出方程求解即可.
解答 解:(Ⅰ)向量$\overrightarrow a$=(1,x),$\overrightarrow b$=(x-3,2),且$\overrightarrow a$⊥$\overrightarrow b$.
可得x-3+2x=0,解得x=1.
(Ⅱ)向量$\overrightarrow a$=(1,1),$\overrightarrow b$=(-1,2),k$\overrightarrow{a}$+$\overrightarrow{b}$=(k-1,k+2),
$\overrightarrow{a}$-2$\overrightarrow{b}$=(3,-3).
k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$平行,
可得:3(k+2)=-3(k-1),解得k=$-\frac{1}{2}$.
点评 本题考查向量共线与向量的垂直体积的应用,考查计算能力.

练习册系列答案
相关题目
9.已知等比数列{an}的前n项和为Sn,若S2=6,S4=30,则S6=( )
| A. | 115 | B. | 116 | C. | 125 | D. | 126 |
6.设点A在-150°角的终边上,|$\overrightarrow{OA}$|=2$\sqrt{2}$(O是坐标原点),则向量$\overrightarrow{OA}$的坐标为( )
| A. | ($\sqrt{6}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{6}$) | C. | (-$\sqrt{2}$,-$\sqrt{6}$) | D. | (-$\sqrt{6}$,-$\sqrt{2}$) |
13.复数z=$\frac{2+i}{1-2i}$的虚部为( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{5}{3}$i | C. | 1 | D. | i |
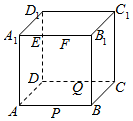 如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法:
如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法: 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”.若输入的m,n分别为385,105,执行该程序框图(图中“mMODn”表示m除以n的余数,例:11MOD7=4),则输出的m等于( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”.若输入的m,n分别为385,105,执行该程序框图(图中“mMODn”表示m除以n的余数,例:11MOD7=4),则输出的m等于( )