题目内容
4．在等差数列{an}中，a5+a6=10，则其前10项和S10的值是（ ）| A． | 10 | B． | 50 | C． | 60 | D． | 100 |
分析 由等差数列性质及前n项和公式代入求解即可．
解答 解：由等差数列性质知，
S10=$\frac{{a}_{1}+{a}_{10}}{2}$×10
=$\frac{{a}_{5}+{a}_{6}}{2}$×10=50，
故选：B．
点评 本题考查了等差数列的性质及前n项和公式．
练习册系列答案
相关题目
15．
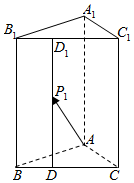如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=AC=$\sqrt{3}$，BC=3，AA1=5，$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$，$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$，$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$，一光线从A射出，第一次射到平面BCC1B1上点P1，经反射后第二次射到表面上点P2，依次下去，…，则P2P3=（ ）
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=AC=$\sqrt{3}$，BC=3，AA1=5，$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$，$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$，$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$，一光线从A射出，第一次射到平面BCC1B1上点P1，经反射后第二次射到表面上点P2，依次下去，…，则P2P3=（ ）| A． | $\frac{\sqrt{10}}{6}$ | B． | $\frac{\sqrt{10}}{4}$ | C． | $\frac{\sqrt{10}}{3}$ | D． | $\frac{\sqrt{10}}{2}$ |
19．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的实轴为A1A2，虚轴的一个端点为B，若三角形A1A2B的面积为$\sqrt{2}$b2，则双曲线的离心率（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{6}}{2}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
9．已知等比数列{an}的前n项和为Sn，若S2=6，S4=30，则S6=（ ）
| A． | 115 | B． | 116 | C． | 125 | D． | 126 |
13．复数z=$\frac{2+i}{1-2i}$的虚部为（ ）
| A． | -$\frac{5}{3}$ | B． | -$\frac{5}{3}$i | C． | 1 | D． | i |
