题目内容
五个岛屿修四座桥(要任意两岛都能沟通),求修桥的总方法数.
考点:排列、组合及简单计数问题
专题:排列组合
分析:如果五个岛屿任意两个都有桥相连,则共需要
=10座桥,从中选出四座,共有:
=210种不同的选法,(1)如果这四座桥只连通四个岛屿,剩下一个岛屿与其它岛屿不连,则共有:
•
5种情况,(2)如果这四座桥连通五个岛屿,但三个相连,另外两个相连,则共有:
•
种情况;除去(1)(2)其它情况均能保证任意两岛都能沟通,相减可得答案.
| C | 2 5 |
| C | 4 10 |
| C | 4 5 |
| C | 4 6 |
| C | 3 5 |
| C | 2 2 |
解答:
解:如果五个岛屿任意两个都有桥相连,则共需要
=10座桥,
从中选出四座,共有:
=210种不同的选法,
(1)如果这四座桥只连通四个岛屿,剩下一个岛屿与其它岛屿不连,
则共有:
•
=75种情况,
(2)如果这四座桥连通五个岛屿,但三个相连,另外两个相连,
则共有:
•
=10种情况;
除去(1)(2)其它情况均能保证任意两岛都能沟通,
故修桥的总方法数有:210-(75+10)=125种.
| C | 2 5 |
从中选出四座,共有:
| C | 4 10 |
(1)如果这四座桥只连通四个岛屿,剩下一个岛屿与其它岛屿不连,
则共有:
| C | 4 5 |
| C | 4 6 |
(2)如果这四座桥连通五个岛屿,但三个相连,另外两个相连,
则共有:
| C | 3 5 |
| C | 2 2 |
除去(1)(2)其它情况均能保证任意两岛都能沟通,
故修桥的总方法数有:210-(75+10)=125种.
点评:本题考查的知识点排列组合,本题从下面解答难度较大,故应该先排除不满足条件的情况,进而由总数相减得到答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
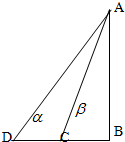 如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于
如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于