题目内容
定义运算a⊕b=
,则函数f(x)=1⊕2x的图象是( )
|
A、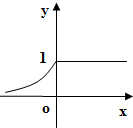 |
B、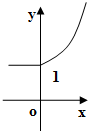 |
C、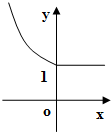 |
D、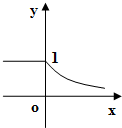 |
考点:函数的图象
专题:函数的性质及应用
分析:从定义运算a⊕b=
上看,对于任意的a、b,a⊕b实质上是求a与b中最大的,再分x≥0与x<0两种情况得函数的解析式.
|
解答:
解:从定义运算a⊕b=
上看,对于任意的a、b,a⊕b实质上是求a与b中最大的,
∴1⊕2x就是取1与2x中较大的一个,
∴对于指数函数y=2x,当x≥0时,2x≥1,∴当x≥0时,f(x)=2x,
当x<0时,2x<1,∴当x<0时,f(x)=1,
故选:B.
|
∴1⊕2x就是取1与2x中较大的一个,
∴对于指数函数y=2x,当x≥0时,2x≥1,∴当x≥0时,f(x)=2x,
当x<0时,2x<1,∴当x<0时,f(x)=1,
故选:B.
点评:对于定义型题目,抓住定义的实质是解题的关键,要注意仔细审题.

练习册系列答案
相关题目
下列说法中不正确的个数是( )
①y=sinx的递增区间是[2kπ,2kπ+
](k∈Z);
②y=sinx在第一象限是增函数;
③y=cosx在[-π,0]上是增函数;
④y=tanx在其定义域上是增函数.
①y=sinx的递增区间是[2kπ,2kπ+
| π |
| 2 |
②y=sinx在第一象限是增函数;
③y=cosx在[-π,0]上是增函数;
④y=tanx在其定义域上是增函数.
| A、1个 | B、2个 | C、3个 | D、4个 |
若a<
,则化简
的结果是( )
| 1 |
| 2 |
| 4 | (2a-1)2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|