题目内容
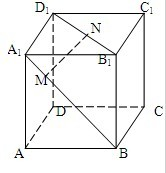 如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.
如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:过点M作ME⊥BB1,垂足为E,连接NE,由题意得Rt△BME∽Rt△BA1B1,Rt△B1NE∽Rt△B1D1B,从而NE∥D1B,进而ME∥AB,由此能证明MN∥平面AC1B.
解答:
证明:过点M作ME⊥BB1,垂足为E,连接NE,
则由题意得Rt△BME∽Rt△BA1B1,
∵BM=2MA1,∴BE=2MA1,
∵D1N=2NB1,∴Rt△B1NE∽Rt△B1D1B,
∴NE∥D1B,
∵ME⊥BB1,AB⊥BB1,∴ME∥AB,
∵NE∩ME=E,D1B∩AB1=B,且NE∥D1B、ME∥AB,
∴面MNE∥面ABC1D1,面ABC1?面ABC1D1中,
即面MNE∥平面AC1B,
∴MN∥平面AC1B.

则由题意得Rt△BME∽Rt△BA1B1,
∵BM=2MA1,∴BE=2MA1,
∵D1N=2NB1,∴Rt△B1NE∽Rt△B1D1B,
∴NE∥D1B,
∵ME⊥BB1,AB⊥BB1,∴ME∥AB,
∵NE∩ME=E,D1B∩AB1=B,且NE∥D1B、ME∥AB,
∴面MNE∥面ABC1D1,面ABC1?面ABC1D1中,
即面MNE∥平面AC1B,
∴MN∥平面AC1B.
点评:本题考查直线与平面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
抛物线y=2ax2(a≠0)焦点坐标是( )
A、(
| ||
B、(0,
| ||
C、(
| ||
D、(0,
|
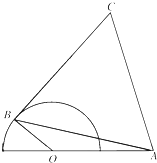 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.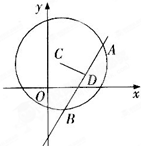 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.