题目内容
下列各点中不在不等式组
表示的平面区域内的是( )
|
| A、(1,1) | ||||
| B、(0,0) | ||||
C、(
| ||||
D、(
|
考点:简单线性规划
专题:不等式的解法及应用
分析:解分别验证点的坐标是否满足不等式组即可得到结论.
解答:
解:A,当x=1,y=1时,x+y=2≤1不成立,故(1,1)不在平面区域内.
B.当x=0,y=0时,x+y=0≤1成立,故(0,0)在平面区域内.
C.当x=
,y=
时,x+y=1≤1成立,故(
,
)在平面区域内.
D.当x=
,y=
时,x+y=
≤1成立,故(
,
)在平面区域内.
故选:A
B.当x=0,y=0时,x+y=0≤1成立,故(0,0)在平面区域内.
C.当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
D.当x=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故选:A
点评:本题主要考查二元一次不等式组表示平面区域,比较基础.

练习册系列答案
相关题目
设集合A={x|(x+3)(x-2)≤0},B={x|y=
},则A∩B( )
| 1 | ||
|
| A、(1,2) |
| B、[1,2] |
| C、[1,2) |
| D、(1,2] |
已知集合U={0,1,2,3,4},A={x|x2-2x=0},则∁UA=( )
| A、{1,2,3} |
| B、{0,1,3,4} |
| C、{1,3,4} |
| D、{0,3,4} |
若实数x,y满足
,则z=x+2y的最小值是( )
|
| A、0 | ||
B、
| ||
| C、5 | ||
| D、1 |
如图,在程序框图中输入n-14,按程序运行后输出的结果是( )


| A、0 | B、2 | C、3 | D、4 |
设复数ω=-
+
i(i为虚数单位),则(ω+1)2=( )
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
圆(x-1)2+(y-1)2=1关于直线y=5x-4对称的圆的方程是( )
| A、(x+1)2+(y+1)2=1 |
| B、(x-1)2+(y-1)2=1 |
| C、(x+1)2+(y-1)2=1 |
| D、(x-1)2+(y+1)2=1 |
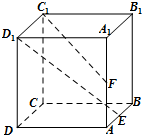 已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点,点M、N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( )
已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点,点M、N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( )