题目内容

ρcosθ+2ρsinθ=1的直角坐标方程为
 
．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：根据直角坐标和极坐标的互化公式x=ρcosθ、y=ρsinθ，把所给曲线的极坐标方程化为直角坐标方程．
解答： 解：根据直角坐标和极坐标的互化公式x=ρcosθ、y=ρsinθ，
可得ρcosθ+2ρsinθ=1的直角坐标方程为x+2y-1=0，
故答案为：x+2y-1=0．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，属于基础题．
练习册系列答案
相关题目
若数列{an}的前n项和为Sn，对任意正整数n都有6Sn=1-2an．
（1）求数列{an}的通项公式；
（2）若c1=0，且对任意正整数n都有cn+1-cn=log 
1
2
an，求证：对任意n≥2，n∈N*都有
1
c2
+
1
c3
+…+
1
cn
＜
3
4
．
先阅读下面的材料：“求
1+
1+
1+…
的值时，采用了如下方法：令
1+
1+
1+…
=x，则有x=
1+x
，两边同时平方，得x2=1+x，解得x=
1+
5
2
（负值舍去）．”----根据以上材料所蕴含的数学思想方法，可以求得函数F（x）=
3+
3+
3+
3+x
-x的零点为
 
．
在极坐标系中，已知圆C经过点P（
2
，
π
4
），圆心为直线ρsin（θ-
π
3
）=-
3
2
与极轴的交点，则圆C的极坐标方程是
 
．
已知函数f（x）=2x2-mx+3，当x∈（-2，+∞）时，函数f（x）为增函数，当x∈（-∞，-2）时，函数f（x）为减函数，则m等于
 
．
若存在正实数M，对于任意x∈（1，+∞），都有|f（x）|≤M，则称函数f（x）在（1，+∞）上是有界函数．下列函数：①f（x）=
1
x-1
；②f（x）=
x
x2+1
；③f（x）=
lnx
x
；④f（x）=xsinx，其中“在（1，+∞）上是有界函数”的序号为
 
．
定义在R上的函数f（x）同时满足性质：①对任何x∈R，均有f（x3）=[f（x）]3成立；②对任何x1，x2∈R，当且仅当x1=x2时，有f（x1）=f（x2）．则f（-1）+f（0）+f（1）的值为
 
．
已知直线AB与抛物线y2=2x交于A，B两点，M是AB的中点，C是抛物线上的点，且使得
CA
•
CB
取最小值，抛物线在点C处的切线为l，则（　　）
A、CM⊥AB
B、CM⊥l
C、CA⊥CB
D、CM=
1
2
AB
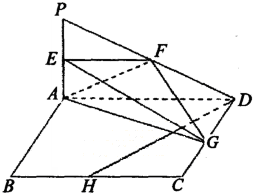如图，四边形ABCD为正方形，PA⊥平面ABCD，且AD=2PA，E、F、G、H分别是线段PA、PD、CD、BC的中点．
（Ⅰ）求证：BC∥平面EFG；
（Ⅱ）求证：DH⊥平面AEG．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网