题目内容
 已知抛物线y2=2px(p>0)的焦点F到直线x-y+1=0的距离为
已知抛物线y2=2px(p>0)的焦点F到直线x-y+1=0的距离为| 2 |
(1)求抛物线的方程;
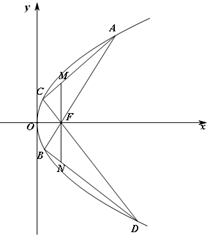
(2)如图,过点F作两条直线分别交抛物线于A、B和C、D,过点F作垂直于x轴的直线分别交AC和BD于点M,N.求证:|MF|=|NF|.
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用抛物线y2=2px(p>0)的焦点F到直线x-y+1=0的距离为
,求出p的值,即可求抛物线的方程;
(2)设直线AB的方程为:x=m1y+1,直线CD的方程为:x=m2y+1,代入抛物线方程,利用韦达定理,求出直线AC、BD的方程,将x=1代入,即可得出结论.
| 2 |
(2)设直线AB的方程为:x=m1y+1,直线CD的方程为:x=m2y+1,代入抛物线方程,利用韦达定理,求出直线AC、BD的方程,将x=1代入,即可得出结论.
解答:
解:(1)焦点F(
,0),由已知得
=
,且p>0,解得p=2,
故所求抛物线的方程为y2=4x.
(2)设直线AB的方程为:x=m1y+1,直线CD的方程为:x=m2y+1,
令A(
,y1),B(
,y2),C(
,y3),D(
,y4)
将x=m1y+1代入抛物线方程得:y2-4m1y-4=0
于是有:y1+y2=4m1,y1y2=-4
同理得:y3+y4=4m2,y3y4=-4,
故A(
,y1),B(
,-
),C(
,y3),D(
,-
)
所以直线AC的方程为:y-y1=
(x-
),①
直线BD的方程为:y-
=-
(x-
),②
将x=1代入①式得:yM=
将x=1代入②式得:yN=-
所以yM=-yN,即:|MF|=|NF|.
| p |
| 2 |
|
| ||
|
| 2 |
故所求抛物线的方程为y2=4x.
(2)设直线AB的方程为:x=m1y+1,直线CD的方程为:x=m2y+1,
令A(
| y12 |
| 4 |
| y22 |
| 4 |
| y32 |
| 4 |
| y42 |
| 4 |
将x=m1y+1代入抛物线方程得:y2-4m1y-4=0
于是有:y1+y2=4m1,y1y2=-4
同理得:y3+y4=4m2,y3y4=-4,
故A(
| y12 |
| 4 |
| 4 |
| y12 |
| 4 |
| y1 |
| y32 |
| 4 |
| 4 |
| y32 |
| 4 |
| y3 |
所以直线AC的方程为:y-y1=
| 4 |
| y1+y3 |
| y12 |
| 4 |
直线BD的方程为:y-
| 4 |
| y1 |
| y1y3 |
| y1+y3 |
| 4 |
| y12 |
将x=1代入①式得:yM=
| 4+y1y3 |
| y1+y3 |
将x=1代入②式得:yN=-
| 4+y1y3 |
| y1+y3 |
所以yM=-yN,即:|MF|=|NF|.
点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查学生的计算能力,难度中等.

练习册系列答案
相关题目
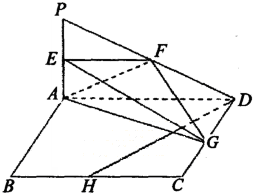 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点. 某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.