题目内容
已知函数f（x）是定义在（0，+∞）上的单调函数，且对任意的x∈（0，+∞）都有f（f（x）-
）=4，则f（4）=（ ）
| 4 |
| x |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：由题意可得f（x）-
为一个常数，令f（x）-
=n，可得f（x）=n+
，且f（n）=4，由已知数据可得n值，进而可得f（4）．
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
解答：
解：∵函数f（x）是定义在（0，+∞）上的单调函数，且f（f（x）-
）=4
∴f（x）-
为一个常数，令f（x）-
=n，可得f（x）=n+
，且f（n）=4
∴n+
=4，解得n=2，∴f（x）=2+
，∴f（4）=3
故选：B
| 4 |
| x |
∴f（x）-
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
∴n+
| 4 |
| n |
| 4 |
| x |
故选：B
点评：本题考查函数的单调性，注意合理地进行等价转化是解决问题的关键，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的三边长可构成公差为1的等差数列，且A＞B＞C，9b=10acosC，则sinA：sinB：sinC=（ ）
| A、4：3：2 |
| B、6：5：4 |
| C、5：4：3 |
| D、5：6：7 |
若复数（m2-1）+（m+1）i为实数（i为虚数单位），则实数m的值为（ ）
| A、-1 | B、0 | C、1 | D、-1或1 |
已知x∈[-
，
]，则函数y=sin4x-cos4x的最小值是（ ）
| π |
| 12 |
| π |
| 3 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
已知定义域为R的函数f（x）在（0，+∞）上为增函数，且函数f（x）为偶函数，则下列结论成立的是 （ ）
| A、f（0）＞f（1） |
| B、f（0）＞f（2） |
| C、f（-1）＞f（2） |
| D、f（-3）＞f（1） |
已知f（x）=（
）x-log2014x，实数a、b、c满足f（a）f（b）f（c）＜0，且0＜a＜b＜c，若实数x0是函数f（x）的一个零点，则下列不等式中，不可能成立的是（ ）
| 1 |
| 2014 |
| A、x0＜a |
| B、x0＞b |
| C、x0＜c |
| D、x0＞c |
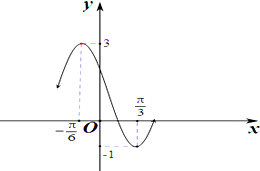已知函数g（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜