题目内容
函数y=sinx•cosx，x∈R的最小正周期是（ ）
| A、4π | ||
B、
| ||
| C、2π | ||
| D、π |
考点：二倍角的正弦,三角函数的周期性及其求法
专题：计算题,三角函数的求值
分析：利用三角函数的倍角公式，将函数进行化简，即可得到结论．
解答：
解：∵y=sinx•cosx=
sin2x，
∴三角函数的周期T=
=π，
故选：D．
| 1 |
| 2 |
∴三角函数的周期T=
| 2π |
| 2 |
故选：D．
点评：本题主要考查三角函数的图象和性质，利用倍角公式将函数进行化简是解决本题的关键．
练习册系列答案
相关题目
已知sina+cosa=
，则sin2a=（ ）
| 1 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知△ABC的三边长可构成公差为1的等差数列，且A＞B＞C，9b=10acosC，则sinA：sinB：sinC=（ ）
| A、4：3：2 |
| B、6：5：4 |
| C、5：4：3 |
| D、5：6：7 |
已知i为虚数单位，则复数z=i（2+i）在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f（x）=
，若f（a）=
，则f（-a）=（ ）
| x2+x+1 |
| x2+1 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
设f（x）是定义在R上且周期为2的函数，在区间[-1，1]上，f（x）=
，其中a，b∈R，若f（
）=f（
），则a+3b=（ ）
|
| 1 |
| 2 |
| 3 |
| 2 |
| A、2 | B、-2 | C、10 | D、-10 |
若复数（m2-1）+（m+1）i为实数（i为虚数单位），则实数m的值为（ ）
| A、-1 | B、0 | C、1 | D、-1或1 |
已知x∈[-
，
]，则函数y=sin4x-cos4x的最小值是（ ）
| π |
| 12 |
| π |
| 3 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
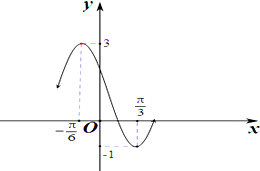已知函数g（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜