题目内容
14.已知函数f(x)的图象如图,则f(x)的解析式为( )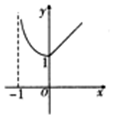
| A. | f(x)=eln|x+1| | B. | f(x)=eln|x-1| | C. | f(x)=e|ln(x+1)| | D. | f(x)=e|ln(x-1)| |
分析 由图象可知函数的定义域R,值域为[1,+∞),可排除C,D,再令x=1可排除B,问题得以解决
解答 解:由图象可知函数的定义域R,值域为[1,+∞),
选项C的定义域为(-1,+∞),选项D的定义域为(1,+∞),
当x=-1时,f(x)=eln|x+1|→+∞,
当x=-1时,f(x)=eln|x-1|=2,
故选:A
点评 本题考查了函数图象的识别,关键掌握函数的定义域和函数值的特点,属于基础题.

练习册系列答案
相关题目
5.给定两个命题p,q,“¬(p∨q)为假”是“p∧q为真”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.若复数z1,z2在复平面内对应的点关于x轴对称,且z1=1+2i,则$\frac{z_1}{z_2}$=( )
| A. | $-\frac{4}{5}+\frac{3}{5}i$ | B. | $-\frac{3}{5}+\frac{4}{5}i$ | C. | $-\frac{1}{2}+\frac{3}{2}i$ | D. | $-\frac{1}{2}-\frac{3}{2}i$ |
3.△ABC内角A,B,C所对的边分别是a,b,c,则“acosA=bcosB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.已知集合A={x|(x-6)(x+2)<0},B={x|x-1>0},则A∩B等于( )
| A. | (1,6) | B. | (-1,6) | C. | (-2,1) | D. | (-1,2) |
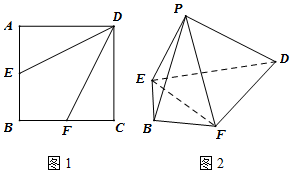 如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.
如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.