题目内容
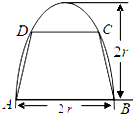 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.(1)求面积S以x为自变量的函数式,并写出其定义域;
(2)求S2的最大值.
考点:导数在最大值、最小值问题中的应用,函数模型的选择与应用
专题:导数的综合应用
分析:(1)以AB的中点O为原点,建立直角坐标系O-xyz,点C的纵坐标y满足方程
+
=1,y≥0,由此能求出面积S以x为自变量的函数式及其定义域.
(2)设f(x)=4(x+r)2(r2-x2),0<x<r,则f′(x)=S(x+r)2(r-2x),令f′(x)=0,得x=
y,由此能求出x=
r时,S2取得最大值
r4.
| x2 |
| r2 |
| x2 |
| 4r2 |
(2)设f(x)=4(x+r)2(r2-x2),0<x<r,则f′(x)=S(x+r)2(r-2x),令f′(x)=0,得x=
| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 4 |
解答:
解:(1)依题意,以AB的中点O为原点,建立直角坐标系O-xyz,如图
则点C的横坐标为x,点C的纵坐标y满足方程
+
=1,y≥0,
解得y=2
,(0<x<r).
∴S=
(2x+2r)•2
=2(x+r)•
,其定义域为{x|0<x<r}.
(2)设f(x)=4(x+r)2(r2-x2),0<x<r,
则f′(x)=S(x+r)2(r-2x),
令f′(x)=0,得x=
y,
∵当0<x<
时,f′(x)>0;当
<x<r时,f′(x)<0.
∴f(x)在(0,
)上是递增函数,在(
,r)上是递减函数,
∴f(
r)是f(x)的最大值,
∴当x=
r时,S2也取得最大值,最大值是
r4.
则点C的横坐标为x,点C的纵坐标y满足方程
| x2 |
| r2 |
| x2 |
| 4r2 |
解得y=2
| r2-x2 |

∴S=
| 1 |
| 2 |
| r2-x2 |
=2(x+r)•
| r2-x2 |
(2)设f(x)=4(x+r)2(r2-x2),0<x<r,
则f′(x)=S(x+r)2(r-2x),
令f′(x)=0,得x=
| 1 |
| 2 |
∵当0<x<
| r |
| 2 |
| r |
| 2 |
∴f(x)在(0,
| r |
| 2 |
| r |
| 2 |
∴f(
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 27 |
| 4 |
点评:本题考查函数的解析式的求法,考查函数的最大值的求法,是中档题,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
相关题目
已知等差数列{an}中,a1+a3=a4=8,则a6的值是( )
| A、10 | B、12 | C、8 | D、16 |
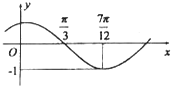 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<