题目内容
 某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.
某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D、E、F,并且,EF∥AB,EF⊥ED(如图1),游客要在△DEF内喂鱼,希望△DEF面积越大越好.设EF=x(米),用x表示△DEF面积S,并求出S的最大值;
(2)现在准备新建造一个走廊,方便游客通行,分别在AB、BC、CA上取点D、E、F,建造正△DEF走廊(不考虑宽度)(如图2),游客希望△DEF周长越小越好.设∠FEC=α,用α表示△DEF的周长L,并求出L的最小值.
考点:解三角形的实际应用
专题:解三角形
分析:(1)通过三角形ABC,求出A,设EF=x,0<x<100,求出CE,BE,表示出三角形的面积,利用二次函数求出最值.
(2)设边长为a,∠FEC=α,α∈(0,
),利用正弦定理求出a的表达式,求出a的最小值,L的最小值.
(2)设边长为a,∠FEC=α,α∈(0,
| π |
| 2 |
解答:
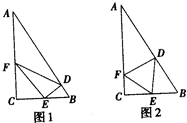 解:(1)直角三角形ABC,∠C=90°,AB=100米,BC=50米
解:(1)直角三角形ABC,∠C=90°,AB=100米,BC=50米
∴sinA=
=
.
A=30°,
∵EF∥AB,EF⊥ED∴∠CFE=30°,
设EF=x,0<x<100,∴CE=
,∴BE=50-
,
∵EF⊥ED,∴EF⊥AB,∴DE=
(50-
),
∴S△ABC=
EF•ED=
x(100-x),
当x=50时,SMAX=
;
(2)设边长为a,∠FEC=α,α∈(0,
),
∴CE=acosα,EB=50-acosα,∠EDB=α,
在三角形DEB中,
=
,
∴a=
=
=
≥
.
∴a的最小值为
,
L的最小值是
.
 解:(1)直角三角形ABC,∠C=90°,AB=100米,BC=50米
解:(1)直角三角形ABC,∠C=90°,AB=100米,BC=50米∴sinA=
| BC |
| AB |
| 1 |
| 2 |
A=30°,
∵EF∥AB,EF⊥ED∴∠CFE=30°,
设EF=x,0<x<100,∴CE=
| x |
| 2 |
| x |
| 2 |
∵EF⊥ED,∴EF⊥AB,∴DE=
| ||
| 2 |
| x |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 8 |
当x=50时,SMAX=
| 625 |
| 2 |
| 3 |
(2)设边长为a,∠FEC=α,α∈(0,
| π |
| 2 |
∴CE=acosα,EB=50-acosα,∠EDB=α,
在三角形DEB中,
| a | ||
sin
|
| 50-acosα |
| sinα |
∴a=
25
| ||||
sinα+
|
25
| ||||
|
50
| ||
| 7sin(α+θ) |
50
| ||
| 7 |
∴a的最小值为
50
| ||
| 7 |
L的最小值是
150
| ||
| 7 |
点评:本题考查三角形的面积的求法,三角函数的最值的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
函数f(x)=2x-cosx在(-∞,+∞)上( )
| A、有最大值 | B、无最大值 |
| C、有最小值 | D、无最值 |
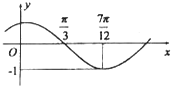 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<