题目内容
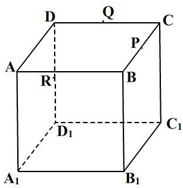 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:①过A1C1且与CD1平行的平面有且只有一个;
②平面PQR截正方体所得截面图形是等腰梯形;
③AC1与QR所成的角为60°;
④线段EF与GH分别在棱A1B1和CC1上运动,且EF+GH=1,则三棱锥E-FGH体积的最大值是
| 1 |
| 12 |
⑤线段MN是该正方体内切球的一条直径,点O在正方体表面上运动,则
| OM |
| ON |
其中真命题的序号是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①转化为A1B,A1C1相交,确定一个平面处理,②可利用补形法,在右侧补充一个正方体,延长或平移,可得截面,③利用三垂线定理可证两线垂直,④利用转化法求解相应体积,可得V三棱锥E-FGH=V三棱锥G-EFC1-V三棱锥H-EFC1,⑤建立空间直角坐标系,利用向量求解.
解答:
解:①CD1∥A1B,A1B∩A1C1=A1,则过A1B,A1C1有且只有一个平面,所以过A1C1且与CD1平行的平面有且只有一个,①正确,
②做RM平行PQ,交BB1于M;做PN平行于QR,交A1D1于NPQRMN这五点所构成的五边形即为截面,②错误;
③连结AC1,DC1,则,DC1为AC1在平面DC1,内的射影,DC1⊥RQ,由三垂线定理可知AC1⊥QR,所成的角为90°,③错误;
④设G在H上方,则V三棱锥E-FGH=V三棱锥G-EFC1-V三棱锥H-EFC1=
×EF×GC1-
×EF×HC1=
×EF×GH,而EF+GH=1,则EF×GH的最大值=
,④正确;
⑤以D1为坐标原点,以D1A1,D1C1,D1D所在直线为x轴,y轴,z轴,建立空间直角坐标系,设正方体内切球球心为S,MN是该内切球的任意一条直径,则
•
=(
+
)•(
+
)=(
+
)•(
-
)=
2-1∈[0,2],⑤正确.
故答案为:①④⑤.
②做RM平行PQ,交BB1于M;做PN平行于QR,交A1D1于NPQRMN这五点所构成的五边形即为截面,②错误;
③连结AC1,DC1,则,DC1为AC1在平面DC1,内的射影,DC1⊥RQ,由三垂线定理可知AC1⊥QR,所成的角为90°,③错误;
④设G在H上方,则V三棱锥E-FGH=V三棱锥G-EFC1-V三棱锥H-EFC1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
⑤以D1为坐标原点,以D1A1,D1C1,D1D所在直线为x轴,y轴,z轴,建立空间直角坐标系,设正方体内切球球心为S,MN是该内切球的任意一条直径,则
| OM |
| ON |
| OS |
| SM |
| OS |
| SN |
| OS |
| SM |
| OS |
| SM |
| OS |
故答案为:①④⑤.
点评:本题以正方体为载体,综合考查线面、面面位置关系,考查线面角、面面角,解题时需要一一进行验证,很容易出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=
的定义域( )
| 1-x |
| A、(-∞,0) |
| B、(-∞,0] |
| C、(0,+∞) |
| D、(-∞,1] |
将边长为a的正方形沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为( )
| A、6a3 | ||||
| B、12a3 | ||||
C、
| ||||
D、
|