题目内容
将边长为a的正方形沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为( )
| A、6a3 | ||||
| B、12a3 | ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:首先利用几何体的边与边的关系求出AE=CE=
a,DE=BE=
a,进一步证明AC⊥平面DEB,最后利用VD-ABC=VC-DEB+VA-DEB,求出几何体的体积.
| ||
| 2 |
| ||
| 2 |
解答:
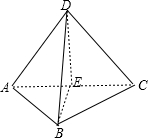 解:依题意:先画出几何体
解:依题意:先画出几何体
边长为a的正方形折叠后,使得BD=a,取AC的中点E,
根据三角形中边的关系,求得:AE=CE=
a,DE=BE=
a
由于AC⊥DE,AC⊥BE
AC⊥平面DEB
所以:VD-ABC=VC-DEB+VA-DEB=2×
•
•
a•
a•
a=
a3
故选:D
 解:依题意:先画出几何体
解:依题意:先画出几何体边长为a的正方形折叠后,使得BD=a,取AC的中点E,
根据三角形中边的关系,求得:AE=CE=
| ||
| 2 |
| ||
| 2 |
由于AC⊥DE,AC⊥BE
AC⊥平面DEB
所以:VD-ABC=VC-DEB+VA-DEB=2×
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 12 |
故选:D
点评:本题考查的知识要点:平面图形与立体图形的转化,锥体的体积公式的应用.

练习册系列答案
相关题目
如下图2,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD=
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )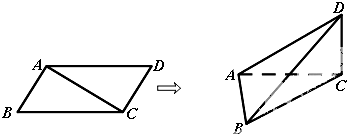
| 5 |

| A、面ABD⊥面BCD |
| B、面ABD⊥面ACD |
| C、面ABC⊥面ACD |
| D、面ABC⊥面BCD |
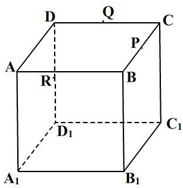 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: