题目内容
设动点A、B(不重合)在椭圆9x2+16y2=144上,椭圆中心为O,且OA⊥OB,则点O到弦AB的距离OH= .
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:分类讨论:当AB⊥x轴或AB∥x轴时,把y=x与椭圆的方程联立即可解出.当AB与x轴不垂直时,设AB的方程为:y=kx+m,A(x1,y1),B(x2,y2).与椭圆方程联立,利用根与系数及其
⊥
?
•
=0,点到直线的距离公式即可得出.
| OA |
| OB |
| OA |
| OB |
解答:
解:当AB⊥x轴或AB∥x轴时,联立
,解得x=y=±
,∴|OH|=
.
当AB与x轴不垂直时,设AB的方程为:y=kx+m,A(x1,y1),B(x2,y2).
联立
,化为(9+16k2)x2+32kmx+16m2-144=0,
△>0.x1+x2=-
,x1x2=
.
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
∵
⊥
,
∴
•
=x1x2+y1y2=
+
+m2=0,
化为25m2=144k2+144.
∴点O到弦AB的距离OH=
=
.
故答案为:
.
|
| 12 |
| 5 |
| 12 |
| 5 |
当AB与x轴不垂直时,设AB的方程为:y=kx+m,A(x1,y1),B(x2,y2).
联立
|
△>0.x1+x2=-
| 32km |
| 9+16k2 |
| 16m2-144 |
| 9+16k2 |
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
∵
| OA |
| OB |
∴
| OA |
| OB |
| (1+k2)(16m2-144) |
| 9+16k2 |
| -32k2m2 |
| 9+16k2 |
化为25m2=144k2+144.
∴点O到弦AB的距离OH=
| |m| | ||
|
| 12 |
| 5 |
故答案为:
| 12 |
| 5 |
点评:本题考查了直线与椭圆相交问题转化为方程联立可得根与系数的关系、向量垂直与数量积的关系、点到直线的距离公式,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
设集合A={x|x≥3},B={x|x2-5x+4≤0},则B∩∁RA=( )
| A、[1,3) |
| B、(-∞,4] |
| C、[3,4] |
| D、[l,+∞) |
如下图2,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD=
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )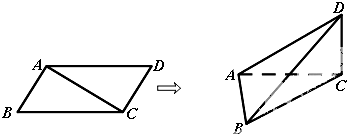
| 5 |

| A、面ABD⊥面BCD |
| B、面ABD⊥面ACD |
| C、面ABC⊥面ACD |
| D、面ABC⊥面BCD |
数列{an}的通项公式为an=ncos
,其前n项和为Sn,则S2015等于( )
| nπ |
| 2 |
| A、1002 | B、1004 |
| C、1006 | D、-1008 |
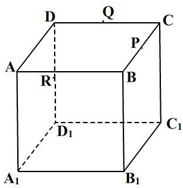 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: