题目内容
已知在等差数列{an}中,Sn为其前n项和,则
,
,
成等差数列,试在等比数列{bn}中写出类似的结论,并给出证明.
| Sn |
| n |
| S2n |
| 2n |
| S3n |
| 3n |
考点:类比推理
专题:推理和证明
分析:类比出结论:等比数列{bn}中bn>0,Tn为其前n项的积,则
,
,
,成等比数列.运用首项,公比具体表示证明即可.
| n | Tn |
| 2n | T2n |
| 3n | T3n |
解答:
解:可以类比出结论:等比数列{bn}中bn>0,Tn为其前n项的积,
则
,
,
,成等比数列.
证明:设首项为b1,公比为q,
=
=a1•q
=
=a1•q
=
=a1•q
∴
=q
,
=q
比值为同一个常数,
∴
,
,
,成等比数列.
则
| n | Tn |
| 2n | T2n |
| 3n | T3n |
证明:设首项为b1,公比为q,
| n | Tn |
| n |
| ||
| n+1 |
| 2 |
| 2n | T2n |
| 2n |
| ||
| 2n+1 |
| 2 |
| 3n | T3n |
| 3n |
| ||
| 3n+1 |
| 2 |
∴
| |||
|
| n |
| 2 |
| |||
|
| n |
| 2 |
比值为同一个常数,
∴
| n | Tn |
| 2n | T2n |
| 3n | T3n |
点评:本题考察了类比推理的思想,属于难题,需要有很好的思维能力,猜想能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正六棱柱的高为6,底面边长为3,则它的体积为( )
| A、48 | ||
B、27
| ||
C、81
| ||
| D、36 |
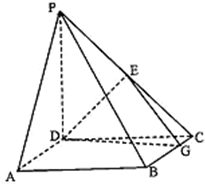 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG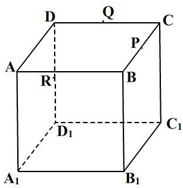 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: