题目内容
函数y=x2-2x+1，x∈[-1，4]的值域是 ．
考点：函数的值域
专题：函数的性质及应用
分析：二次函数的性质可判断：最大值为f（4），最小值为f（1）．
解答：
解：∵函数y=x2-2x+1，x∈[-1，4]，
∴对称轴x=1，
根据二次函数的性质可判断：
最大值为f（4）=9，最小值为f（1）=0，
∴的值域是[0，9]
故答案为：[0，9]
∴对称轴x=1，
根据二次函数的性质可判断：
最大值为f（4）=9，最小值为f（1）=0，
∴的值域是[0，9]
故答案为：[0，9]
点评：本题考查了二次函数的性质运用求解最值问题，属于容易题．
练习册系列答案
相关题目
下列三个图象中能表示y是x的函数图象的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
设集合A={x|x≥3}，B={x|x2-5x+4≤0}，则B∩∁RA=（ ）
| A、[1，3） |
| B、（-∞，4] |
| C、[3，4] |
| D、[l，+∞） |
函数y=（
）x2-2的单调递减区间为（ ）
| 1 |
| 2 |
| A、（-∞，0] | ||
| B、[0，+∞） | ||
C、（-∞，
| ||
D、[
|
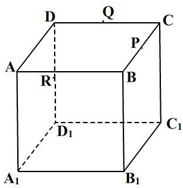如图，正方体ABCD-A1B1C1D1的棱长为2，P，Q，R分别是棱BC，CD，DD1的中点．下列命题：