题目内容
已知函数f(x)满足f(logax)=
(x-x-1),其中a>0,且a≠1.
(1)求函数y=f(x)的解析式,并判断其奇偶性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求实数a的取值范围.
| a |
| a2-1 |
(1)求函数y=f(x)的解析式,并判断其奇偶性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求实数a的取值范围.
考点:函数恒成立问题,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)换元法:令t=logax,则x=at,代入函数式可得解析式,利用奇偶函数的定义可判断;
(2)分a>1和0<a<1两种情况对函数的单调性进行讨论,
当x∈(-∞,2)时,f(x)-4的值恒为负数,等价于f(x)-4<0恒成立,也即f(x)<4恒成立,利用函数的单调性可作出判断;
(2)分a>1和0<a<1两种情况对函数的单调性进行讨论,
当x∈(-∞,2)时,f(x)-4的值恒为负数,等价于f(x)-4<0恒成立,也即f(x)<4恒成立,利用函数的单调性可作出判断;
解答:
解:(1)令logax=t则x=at,
∴f(t)=
(at-a-t),
∴f(x)=
(ax-a-x);
∵f(-x)=
(a-x-ax)=-f(x),
∴f(x)为奇函数;
(2)当a>1时,a-x递减,-a-x递增,ax递增,所以ax-a-x递增,
又
>0,所以f(x)在R上递增;
当0<a<1时,a-x递增,-a-x递减,且ax递减,所以ax-a-x递减,
又
<0,故此时f(x)递增;
综上,当a>0且a≠1时,f(x)在R上递增.
当x∈(-∞,2)时,f(x)-4的值恒为负数,等价于f(x)-4<0恒成立,也即f(x)<4恒成立,
因为y=f(x)在(-∞,2)上单调递增,f(x)<f(2)=
(a2-a-2)=
,
所以
≤4,
∴2-
≤a≤2+
又a>0,a≠1,故a∈[2-
,1)∪(1,2+
]
∴f(t)=
| a |
| a2-1 |
∴f(x)=
| a |
| a2-1 |
∵f(-x)=
| a |
| a2-1 |
∴f(x)为奇函数;
(2)当a>1时,a-x递减,-a-x递增,ax递增,所以ax-a-x递增,
又
| a |
| a2-1 |
当0<a<1时,a-x递增,-a-x递减,且ax递减,所以ax-a-x递减,
又
| a |
| a2-1 |
综上,当a>0且a≠1时,f(x)在R上递增.
当x∈(-∞,2)时,f(x)-4的值恒为负数,等价于f(x)-4<0恒成立,也即f(x)<4恒成立,
因为y=f(x)在(-∞,2)上单调递增,f(x)<f(2)=
| a |
| a2-1 |
| a2+1 |
| a |
所以
| a2+1 |
| a |
∴2-
| 3 |
| 3 |
又a>0,a≠1,故a∈[2-
| 3 |
| 3 |
点评:本题主要考查函数的奇偶性与单调性,利用函数的单调性求函数在某区间上的最值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=(
)x2-2的单调递减区间为( )
| 1 |
| 2 |
| A、(-∞,0] | ||
| B、[0,+∞) | ||
C、(-∞,
| ||
D、[
|
已知正六棱柱的高为6,底面边长为3,则它的体积为( )
| A、48 | ||
B、27
| ||
C、81
| ||
| D、36 |
一个盛满水的三棱锥容器S-ABC中,不久发现三条侧棱上各有一个小洞D,E,F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )
A、
| ||
B、
| ||
C、
| ||
D、
|
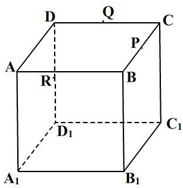 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: