题目内容
设正项等比数列{an},已知前n项积为Tn,若T10=9T6,则a5•a12的值为 .
考点:等比数列的性质
专题:等差数列与等比数列
分析:由已知条件推导出
=a7a8a9a10=(a5a12)2=9,由此能求出a5 •a12的值.
| T10 |
| T6 |
解答:
解:∵正项等比数列{an},前n项积为Tn,T10=9T6,
∴
=a7a8a9a10=(a5a12)2=9,
∴a5 •a12=3.
故答案为:3.
∴
| T10 |
| T6 |
∴a5 •a12=3.
故答案为:3.
点评:本题考查等比数列的两项积的求法,是基础题,解题时要认真审题,注意等比数列的通项公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知直线l的方程为2x-2y+b=0(b∈R),则直线l的倾斜角为( )
| A、30° | B、45° |
| C、135° | D、与b有关 |
已知点M(a,b)在直线3x+4y=10上,则
的最小值为( )
| a2+b2 |
| A、2 | ||
| B、3 | ||
C、
| ||
| D、5 |
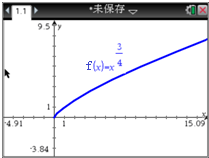 某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=
某同学利用TI-Nspire图形计算器作图作出幂函数f(x)= 在正方体ABCD-A1B1C1D1中,直线A1B和平面A1B1C1D1所成的角为
在正方体ABCD-A1B1C1D1中,直线A1B和平面A1B1C1D1所成的角为