题目内容
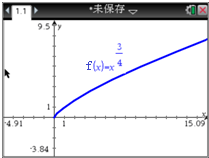 某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=x
某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=x| 3 |
| 4 |
| 3 |
| 4 |
考点:幂函数的性质
专题:函数的性质及应用
分析:由图象知f(x)=x
在区间[1,4]上是增函数,由此能求出f(x)=x
在区间[1,4]上的最大值.
| 3 |
| 4 |
| 3 |
| 4 |
解答:
 解:如图,结合幂函数f(x)=x
解:如图,结合幂函数f(x)=x
的图象,
知f(x)=x
在区间[1,4]上是增函数,
∴f(x)=x
在区间[1,4]上的最大值为:
f(4)=4
=2
=2
.
故答案为:2
.
 解:如图,结合幂函数f(x)=x
解:如图,结合幂函数f(x)=x| 3 |
| 4 |
知f(x)=x
| 3 |
| 4 |
∴f(x)=x
| 3 |
| 4 |
f(4)=4
| 3 |
| 4 |
| 3 |
| 2 |
| 2 |
故答案为:2
| 2 |
点评:本题考查幂函数的性质的应用,是基础题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
函数f(x)=
sin(ωx+φ)(x∈R,ω>0,|φ|<
)的部分图象如图所示,则ω,φ的值分别是( )
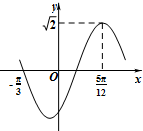
| 2 |
| π |
| 2 |

A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|