题目内容
已知直线l的方程为2x-2y+b=0（b∈R），则直线l的倾斜角为（ ）
| A、30° | B、45° |
| C、135° | D、与b有关 |
考点：直线的倾斜角
专题：直线与圆
分析：利用直线方程先求出直线的斜率，再由正切函数求出直线的斜率．
解答：
解：∵直线l的方程为2x-2y+b=0（b∈R），
∴直线l的斜率k=1，
∴直线l的倾斜角α=45°．
故选：B．
∴直线l的斜率k=1，
∴直线l的倾斜角α=45°．
故选：B．
点评：本题考查直线的倾斜角的求法，是基础题，解题时要认真审题，注意正切函数的合理运用．
练习册系列答案
相关题目
如图，在Rt△ADE中，B是斜边AE的中点，以AB为直径的圆O与边DE相切于点C，若AB=3，则线段CD的长为双曲线
-
=1（a＞0，b＞0），右焦点F2（c，0），A（-a，0），若F2到直线y=
x的距离等于A点到直线y=
x距离的2倍，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b |
| a |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
若实数x，y满足不等式组
且z=x+3y的最大值为12，则实数k=（ ）
|
| A、-12 | ||
B、-
| ||
| C、-9 | ||
D、-
|
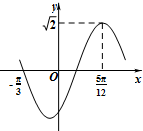
函数f（x）=
sin（ωx+φ）（x∈R，ω＞0，|φ|＜
）的部分图象如图所示，则ω，φ的值分别是（ ）
| 2 |
| π |
| 2 |
A、2，-
| ||
B、2，-
| ||
C、4，-
| ||
D、4，
|
已知集合A={y|y=(
)x2+1，x∈R}，则满足A∩B=B的集合B可以是（ ）
| 1 |
| 2 |
A、{0，
| ||
| B、{x|-1≤x≤1} | ||
C、{x|0＜x＜
| ||
| D、{x|x＞0} |