题目内容
已知点M（a，b）在直线3x+4y=10上，则
的最小值为（ ）
| a2+b2 |
| A、2 | ||
| B、3 | ||
C、
| ||
| D、5 |
考点：基本不等式
专题：不等式的解法及应用
分析：由于点M（a，b）在直线l：3x+4y=10上，而
表示点M（a，b）与原点的距离．因此要求的
的最小值转化为原点到此直线的距离即可．
| a2+b2 |
| a2+b2 |
解答：
解：∵点M（a，b）在直线l：3x+4y=10上，
而
表示点M（a，b）与原点的距离，
因此当OM⊥l时，
取得最小值．
∴(
)min=
=2．
故选：A．
而
| a2+b2 |
因此当OM⊥l时，
| a2+b2 |
∴(
| a2+b2 |
| |0+0-10| | ||
|
故选：A．
点评：本题考查了点到直线的距离公式、转化思想方法，属于中档题．
练习册系列答案
天天向上口算本系列答案
相关题目
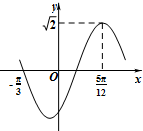
函数f（x）=
sin（ωx+φ）（x∈R，ω＞0，|φ|＜
）的部分图象如图所示，则ω，φ的值分别是（ ）
| 2 |
| π |
| 2 |
A、2，-
| ||
B、2，-
| ||
C、4，-
| ||
D、4，
|
已知集合A={y|y=(
)x2+1，x∈R}，则满足A∩B=B的集合B可以是（ ）
| 1 |
| 2 |
A、{0，
| ||
| B、{x|-1≤x≤1} | ||
C、{x|0＜x＜
| ||
| D、{x|x＞0} |
均值都是5的四组数据条形图如下，将四组数据作比较，错误的是（ ）
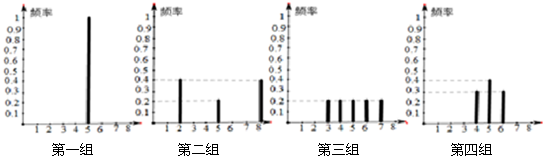
| A、第一组标准差最小 |
| B、第二组极差最大 |
| C、第三组最稳定 |
| D、第三组的方差大于第四组的方差 |
已知
=(2，2)，
=(4，1)，
=(x，0)，则当
•
最小时x的值是（ ）
| OA |
| OB |
| OP |
| AP |
| BP |
| A、-3 | B、3 | C、-1 | D、1 |
直线l经过坐标原点和点（-1，-1），则直线l的倾斜角是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|