题目内容
四棱锥P-ABCD的底面ABCD是边长为2的正方形，PA⊥底面ABCD且PA=4，则PC与底面ABCD所成角的正切值为 ．
考点：直线与平面所成的角
专题：计算题,空间角
分析：先根据条件找出直线PA与底面ABCD所成角，连接AC，则∠PCA就是直线PC与底面ABCD所成角，在直角三角形PAC中求出此角即可．
解答：
解：连接AC，则
∵PA⊥底面ABCD，
∴∠PCA是PC与底面ABCD所成角，
∵四棱锥P-ABCD的底面ABCD是边长为2的正方形，
∴AC=2
，
∵PA=4，
∴tan∠PCA=
=
=
．
故答案为：
．
解：连接AC，则∵PA⊥底面ABCD，
∴∠PCA是PC与底面ABCD所成角，
∵四棱锥P-ABCD的底面ABCD是边长为2的正方形，
∴AC=2
| 2 |
∵PA=4，
∴tan∠PCA=
| PA |
| AC |
| 4 | ||
2
|
| 2 |
故答案为：
| 2 |
点评：本题主要考查了直线与平面垂直的性质，以及直线与平面所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
如图，在Rt△ADE中，B是斜边AE的中点，以AB为直径的圆O与边DE相切于点C，若AB=3，则线段CD的长为双曲线
-
=1（a＞0，b＞0），右焦点F2（c，0），A（-a，0），若F2到直线y=
x的距离等于A点到直线y=
x距离的2倍，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b |
| a |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
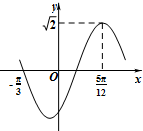
函数f（x）=
sin（ωx+φ）（x∈R，ω＞0，|φ|＜
）的部分图象如图所示，则ω，φ的值分别是（ ）
| 2 |
| π |
| 2 |
A、2，-
| ||
B、2，-
| ||
C、4，-
| ||
D、4，
|
直线l经过坐标原点和点（-1，-1），则直线l的倾斜角是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|