题目内容
设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.则P(ξ=0)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:从棱长为1的正方体的12条棱中任取两条,共有
种了法,若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,共有8
对相交棱,由此能求出P(ξ=0).
| C | 2 12 |
| C | 2 3 |
解答:
解:从棱长为1的正方体的12条棱中任取两条,
共有
种了法,
若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,
∴共有8
对相交棱,
∴P(ξ=0)=
=
.
故选:B.
共有
| C | 2 12 |
若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,
∴共有8
| C | 2 3 |
∴P(ξ=0)=
8
| ||
|
| 4 |
| 11 |
故选:B.
点评:本题以正方体为载体考查概率的求法,是中档题,把概率和立体几何融为一体,是一道好题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
独立性检验中,假设H0:变量X与变量Y没有关系,则在H0成立的情况下,P(K2≥6.635)≈0.010表示的意义是( )
| A、在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y有关” |
| B、在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y无关” |
| C、有99%以上的把握认为“变量X与变量Y无关 |
| D、有99%以上的把握认为“变量X与变量Y有关” |
设函数f(x)=ex-ax,若f′(0)=2,则a的值为( )
| A、-1 | B、0 | C、1 | D、3 |
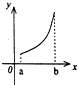
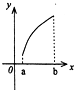
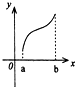
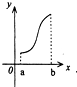
给出下列三个函数的图象:
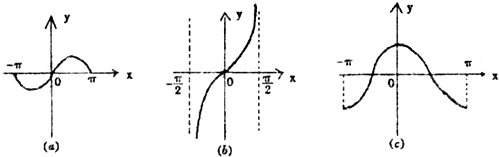
它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )

它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
| f(x)+f(y) |
| 1-f(x)f(y) |
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )
| A、(a)-①,(b)-②,(c)-③ |
| B、(b)-①,(c)-②,(a)-③ |
| C、(c)-①,(b)-②,(a)-③ |
| D、(a)-①,(c)-②,(b)-③ |
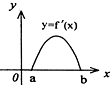 设f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
设f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )