Question

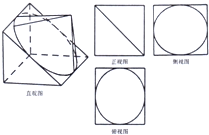某几何体是直三棱柱与圆锥的组合体，其直观图和三视图如图所示，正视图为正方形，其中俯视图中椭圆的离心率为

 

．

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：根据三视图的性质得到俯视图中椭圆的短轴长和长周长，再根据椭圆的性质a²-b²=c²，和离心率公式e=

c

a

，计算即可．

解答： 解：设正视图正方形的边长为m，根据正视图与俯视图的长相等，得到俯视图中椭圆的短轴长2b=m，
俯视图的宽就是圆锥底面圆的直径

2

m，得到俯视图中椭圆的长轴长2a=

2

m，
则椭圆的焦距c=

a2-b2

=

1

2

m，
根据离心率公式得，e=

c

a

=

2

2

故答案为：

2

2

．

点评：本题主要考查了椭圆的离心率公式，以及三视图的问题，属于基础题．