题目内容
设互不相等的平面向量组
（i∈N*）满足条件：①|
|=1；②
•
=0．若记
=
+
+…+
（n≥2），则|
|的取值集合为 ．
| ai |
| ai |
| ai |
| ai+1 |
| Sn |
| a1 |
| a2 |
| an |
| Sn |
考点：数列的求和,平面向量数量积的运算
专题：平面向量及应用
分析：根据条件，分别讨论当n取不同数值时，对应的结果即可得到结论．
解答：
解：∵①|
|=1；②
•
=0．
∴
的取值具备周期性，周期数为4，
不妨设
=（1，0），
=（0，1），
=(-1，0)，
=(0，-1)，
则
=
+
=（1，1），则|
|=
，
=
+
+
=
，则|
|=1，
=
+
+
+
=（0，0），则|
|=0，
=
+
+
+
+
=
，则|
|=|
|=1，
故|
|的取值集合为{0，1，
}，
故答案为：{0，1，
}
解：∵①|| ai |
| ai |
| ai+1 |
∴
| Sn |
不妨设
| a1 |
| a2 |
| a3 |
| a4 |
则
| S2 |
| a1 |
| a2 |
| S2 |
| 2 |
| S3 |
| a1 |
| a2 |
| a3 |
| a2 |
| S3 |
| S4 |
| a1 |
| a2 |
| a3 |
| a4 |
| S4 |
| S5 |
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| a5 |
| S5 |
| a5 |
故|
| Sn |
| 2 |
故答案为：{0，1，
| 2 |
点评：本题主要考查平面向量的基本运算，根据向量的特点得到向量取值的周期性是解决本题的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
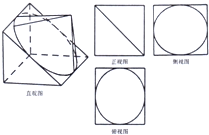某几何体是直三棱柱与圆锥的组合体，其直观图和三视图如图所示，正视图为正方形，其中俯视图中椭圆的离心率为