题目内容
已知（2x-xlgx）8的展开式中，二项式系数最大的项的值等于1120，则实数x的值为 ．
考点：二项式系数的性质
专题：计算题,二项式定理
分析：直接利用二项展开式二项式系数最大的项的值等于1120，列出方程求出x的值．
解答：
解：（2x-xlgx）8的展开式中，二项式系数最大的项是第5项，
所以
(2x)4(xlgx)4=1120．
即x（4+4lgx）=1，
所以4+4lgx=0，或x=1
所以x=
，或x=1，
故答案为：x=1或x=
．
所以
| C | 4 8 |
即x（4+4lgx）=1，
所以4+4lgx=0，或x=1
所以x=
| 1 |
| 10 |
故答案为：x=1或x=
| 1 |
| 10 |
点评：本题考查二项式系数的性质，考查指数对数方程的解法，考查计算能力．
练习册系列答案
导学全程练创优训练系列答案
相关题目
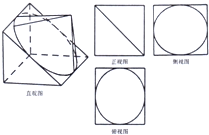某几何体是直三棱柱与圆锥的组合体，其直观图和三视图如图所示，正视图为正方形，其中俯视图中椭圆的离心率为