题目内容
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a,b的值分别为( )


| A、0.27,78 |
| B、54,0.78 |
| C、27,0.78 |
| D、54,78 |
考点:等比数列的性质,等差数列的性质
专题:计算题,等差数列与等比数列
分析:由直方图可以求前两组的频数,由此知道前四组的前两项,故可由等比数列的性质求得前四组的频数,进而可求出后六组的频数和以及等差数列首项,由此可求出最后一组的频数,则a,b可求出
解答:
解:由题意第一组的频率是0.01,第二组的频率是0.03,故两两组的频数是200×0.01=2,200×0.03=6,
由于前4组的频数成等比数列,故其公比是3,故第三组的频数是18,第四组频数是54,由图知a=54,由此知前三组频数和为26,故后六组频数和为174
又后六组的频数成等差数列,设最后一组的频数为x则有
×6=174得x=4
令后六组的公差为d,则有5d=4-54=-50,d=-10,故后组的频数依次是44,34,24,14,4
由此得视力在4.6到5.0之间的频数是156,故b=0.78
故选:B.
由于前4组的频数成等比数列,故其公比是3,故第三组的频数是18,第四组频数是54,由图知a=54,由此知前三组频数和为26,故后六组频数和为174
又后六组的频数成等差数列,设最后一组的频数为x则有
| 54+x |
| 2 |
令后六组的公差为d,则有5d=4-54=-50,d=-10,故后组的频数依次是44,34,24,14,4
由此得视力在4.6到5.0之间的频数是156,故b=0.78
故选:B.
点评:本题考查识图用图的能力,间接考查了等比数列与等差数列的性质,注意理清数列在此处与统计衔接的方式

练习册系列答案
相关题目
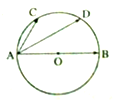
如图,已知AB是圆O的直径,点C,D等分
,已知
=
,
=
,则
等于( )
 |
| AB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知i是虚数单位,则化简复数
的结果为( )
| -1+i |
| 1+i |
| A、i | B、-1 | C、-i | D、1 |
A、B是双曲线
-
=1右支上的两点,若弦AB的中点到Y轴的距离是4,则|AB|的最大值为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、2 | B、4 | C、6 | D、8 |
已知点P是双曲线
-
=1上一点,M,N是双曲线的左,右顶点,若直线PM的斜率的取值范围是[2,3],则直线PN的斜率的取值范围是( )
| x2 |
| 4 |
| y2 |
| 12 |
A、[1,
| ||||
B、[
| ||||
C、[
| ||||
D、[2,
|
执行如图所示的程序框图,则输出的a=( )


A、
| ||
B、-
| ||
| C、5 | ||
D、
|
某几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|