题目内容

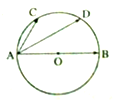
如图，已知AB是圆O的直径，点C，D等分
AB
，已知
AB
=
a
，
AC
=
b
，则
AD
等于（　　）
A、
a
-
1
2
b
B、
1
2
a
-
b
C、
a
+
1
2
b
D、
1
2
a
+
b
考点：向量的加法及其几何意义,向量的减法及其几何意义
专题：平面向量及应用
分析：先证明
CD
=
AO
，再利用向量的加法进行表示
AD
即可．
解答： 解：连接CD，0D，则AC=OD，
又已知AB是圆O的直径，点C，D等分
AB
，
所以∠CAD=∠DOB，
∴四边形AODC是平行四边形，
∴
CD
=
AO
=
1
2
a
，
∴
AD
=
1
2
a
+
b
．
故选D．
点评：本题主要考查向量的加法运算以及向量的相等等概念，属于基础题．
练习册系列答案
相关题目
如图程序框图是计算22+42+…++1 0002的值，程序框图中条件语句中应填写
 
（只能写含1000的式子）
若函数f（x）=
x3
3
-
ax2
2
+x+1在区间（
1
2
，3）上有极值点，则实数a的取值范围为
 
．
已知（x-1）2+y2=1，点A（-2，0）及点B（3，a），从点A观察点B，要使视线不被圆挡住，则a的取值范围
 
．
如图，已知R是实数集，集合A={x|log
1
2
（x-1）＞0}，B={x|
2x-3
x
＜0}，则阴影部分表示的集合是（　　）
A、[0，1]
B、[0，1）
C、（0，1）
D、（1，
3
2
]
(1-2sin21)(2cos21-1)
等于（　　）
A、cos2
B、-cos2
C、cos
1
2
D、-cos
1
2
已知点A为圆C：x2+y2-4x-6y+12=0上的动点，另外一个动点P满足PA与圆C相切，且|PA|=
3
；直线y=kx+3与点P的轨迹相交于M，N两点，若|MN|≥2
3
，则实数k的取值范围是（　　）
A、[-
3
3
，
3
3
]
B、[-
3
4
，0]
C、[-
3
，
3
]
D、[-
2
3
，0]
为了解某校高三学生的视力情况，随机地抽查了该校200名高三学生的视力情况，得到频率分布直方图，如右，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最多一组学生数为a，视力在4.6到5.0之间的频率为b，则a，b的值分别为（　　）
A、0.27，78
B、54，0.78
C、27，0.78
D、54，78
已知函数f（x）=3x+x-5的零点x0∈[a，b]，且b-a=1，a，b∈N*，则a+b=（　　）
A、-2B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网