Question

过椭圆

x2

a

+

y2

b

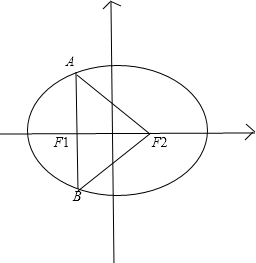
=1（a＞b＞0）的左焦点F₁作x轴的垂线交椭圆于A、B两点，F₂为右焦点，若△ABF₂为等腰直角三角形，则该椭圆的离心率为

 

．

Answer 1

考点：椭圆的简单性质

专题：

分析：设F₁（-c，0），根据已知条件容易判断|AF₁|=|F₁F₂|=2c，这样即可求得A点坐标，并带入椭圆方程得到：

c2

a

+

4c2

b

=1，又c²=a-b，带入即可用b表示a：a=

1+ 2

2

b，带入c²=a-b得c2=

2 -1

2

b，所以

c2

a

=(

2

-1)2，这样即可求出离心率．

解答： 解：如图，设F₁（-c，0），△ABF₂为等腰直角三角形，∴∠AF₂B=90°，∠AF₂F₁=45°，∴△AF₂F₁为等腰直角三角形；
∴|AF₁|=|F₁||F₂|=2c，∴A（-c，2c）；
∴将A点坐标带入椭圆方程得：

c2

a

+

4c2

b

=1，又c²=a-b，∴

a-b

a

+

4(a-b)

b

=1，将该等式变成：
4a²-4ba-b²=0，把该等式看成关于a的方程，解方程得：a=

(1+ 2 )b

2

，或

(1- 2 )b

2

(舍去)；
∴c2=a-b=

( 2 -1)b

2

，∴

c2

a

=(

2

-1)2；
∴该椭圆离心率为：

2

-1．

点评：考查椭圆的标准方程，椭圆上的点和椭圆方程的关系，椭圆的离心率及计算公式：e=

c

a

．