题目内容
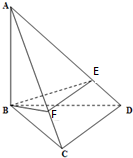如图，在四面体ABCD中，AB⊥平面BCD，∠BCD=90°，点E是线段AD上一点（不与线段AD重合），F是点B在线段AC上的射影，求证：平面BEF⊥平面ACD．考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：由已知，得BF⊥CD，由BF⊥AC，知BF⊥平面ACD，由此能够证明平面BEF⊥平面ACD．
解答：
证明：∵AB⊥平面BCD，
∴AB⊥CD，
∵CD⊥BC且AB∩BC=B，
∴CD⊥平面ABC．
∴CD⊥BF，
∵BF⊥AC，AC∩CD=D
∴BF⊥平面ACD
又BF在平面BEF内，
∴平面BEF⊥平面ACD．
∴AB⊥CD，
∵CD⊥BC且AB∩BC=B，
∴CD⊥平面ABC．
∴CD⊥BF，
∵BF⊥AC，AC∩CD=D
∴BF⊥平面ACD
又BF在平面BEF内，
∴平面BEF⊥平面ACD．
点评：本题主要考察了平面与平面垂直的判定，属于基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
根据如下数据：
得到回归方程为
=bx+a，则ab的值（ ）
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| ∧ |
| y |
| A、大于0 | B、等于0 |
| C、小于0 | D、不能确定 |