题目内容
若二次函数y=ax2+bx+c在区间[0，+∞）上是减函数，则点P（a，b）在平面直角坐标系中位于 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：由二次函数y=ax2+b在区间[0，+∞）上是减函数，可得函数的图象开口朝下，即a＜0；且对称轴x=-
≤0，进而可得点P（a，b）在平面直角坐标系中的位置．
| b |
| 2a |
解答：
解：∵二次函数y=ax2+bx+c在区间[0，+∞）上是减函数，
故函数的图象开口朝下，
∴a＜0；
且对称轴x=-
≤0，
∵a＜0，
∴b≤0，
所以点（a，b）在平面直角坐标系中位于：第三象限或x轴负半轴；
故答案为：第三象限或x轴负半轴
故函数的图象开口朝下，
∴a＜0；
且对称轴x=-
| b |
| 2a |
∵a＜0，
∴b≤0，
所以点（a，b）在平面直角坐标系中位于：第三象限或x轴负半轴；
故答案为：第三象限或x轴负半轴
点评：本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
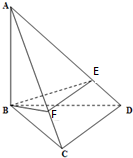如图，在四面体ABCD中，AB⊥平面BCD，∠BCD=90°，点E是线段AD上一点（不与线段AD重合），F是点B在线段AC上的射影，求证：平面BEF⊥平面ACD．
