题目内容
一个四面体的三视图如图所示，则该四面体的四个面中最大的面积是 ．
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据三视图，得到四面体的直观图，然后判断四个面中的最大面积即可．
解答：
解：将该几何体放入边长为2的正方体中，由三视图可知该四面体为D-BD1C1，（左边为正前方），由直观图可知，最大的面为BDC1．
在正三角形BDC1中，BD=2
，
所以面积S=
×(2
)2×
=2
．
故答案为：2
．
解：将该几何体放入边长为2的正方体中，由三视图可知该四面体为D-BD1C1，（左边为正前方），由直观图可知，最大的面为BDC1．在正三角形BDC1中，BD=2
| 2 |
所以面积S=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
故答案为：2
| 3 |
点评：本题主要考查三视图的识别和判断，将几何体放入正方体中去研究，是解决本题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
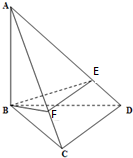如图，在四面体ABCD中，AB⊥平面BCD，∠BCD=90°，点E是线段AD上一点（不与线段AD重合），F是点B在线段AC上的射影，求证：平面BEF⊥平面ACD．