题目内容
若函数y=cos（
+φ）（0＜φ＜π）的一条对称轴方程为x=
，求函数y=sin（2x-φ）（0≤x＜π）的单调增区间．
| x |
| 3 |
| 9π |
| 4 |
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：根据函数y=cos（
+φ）（0＜φ＜π）的一条对称轴方程为x=
，得出φ=
，即求解不等式-
≤2x-
≤
π，即可得出数单调增区间[
，
]．
| x |
| 3 |
| 9π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 7 |
| 4 |
| 3π |
| 8 |
| 7π |
| 8 |
解答：
解：∵函数y=cos（
+φ）（0＜φ＜π）的一条对称轴方程为x=
，
∴
+φ=kπ，∈z，φ=kπ-
，k∈z，
∵0≤φ＜π，
∴φ=
，
∵函数y=sin（2x-φ）=sin（2x-
）（0≤x＜π）
-
≤2x-
≤
π，
∴
≤2x-
≤
，
∴
≤x≤
，
∴函数单调增区间[
，
]．
| x |
| 3 |
| 9π |
| 4 |
∴
| 3π |
| 4 |
| 3π |
| 4 |
∵0≤φ＜π，
∴φ=
| π |
| 4 |
∵函数y=sin（2x-φ）=sin（2x-
| π |
| 4 |
-
| π |
| 4 |
| π |
| 4 |
| 7 |
| 4 |
∴
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
∴
| 3π |
| 8 |
| 7π |
| 8 |
∴函数单调增区间[
| 3π |
| 8 |
| 7π |
| 8 |
点评：本题考查了正弦函数，余弦函数的图象和性质，结合不等式求解，属于中档题．
练习册系列答案
相关题目
过原点的椭圆的一个焦点为F（1，0），其长轴长为4，则椭圆中心的轨迹方程是（ ）
A、（x-
| ||||
B、（x+
| ||||
C、x2+（y-
| ||||
D、x2+（y+
|
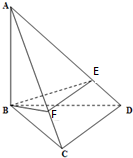如图，在四面体ABCD中，AB⊥平面BCD，∠BCD=90°，点E是线段AD上一点（不与线段AD重合），F是点B在线段AC上的射影，求证：平面BEF⊥平面ACD．